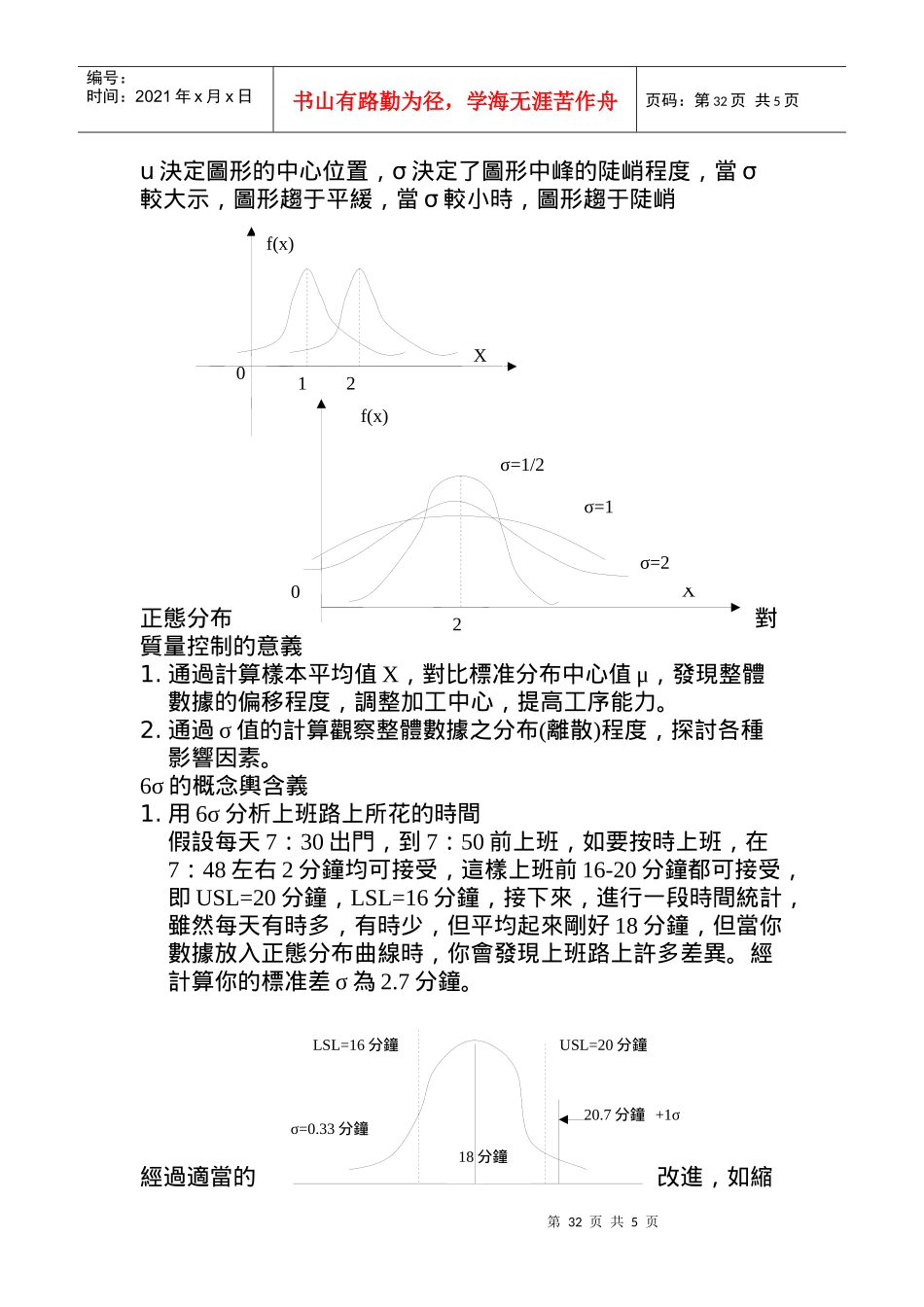
第31页共5页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第31页共5页6σ輿正態分布輿質量相關得數學統計知識主要包括三個方面,即正態分布、二項分布、和泊松分布。二個分析即回歸輿相關分析、方差分析和假設檢驗,這里只介紹正態分布。正態分布正態分布又稱概率分布,產品的諸多品質指標(如尺寸、強度、硬度等)都是從于正態分布的。如果影響某一變量的隨機因素很多,而每一個都不起決定作用,且這些影響是可以疊加的,那么隨機變量被認為是順從正態分布的。設隨機變量的概率密度為:-∞0則稱X服從參數為(u,σ*σ)的正態分布,記為X~N(u,σ*σ)驗証P(x)是一個密度函數當u=0,σ=1時,稱x為標准正態分布,記為X~N(0,1)其概率密度和分布函數分別用Y(x),φ(x)表示Y(x)=[1/√(2π)]*e-x*x/2φ(x)=[1/√(2π)]∫-∞xe-u*u/2du一般正態分布成標准正態分布:F(x)=P{Xx}=[1/√(2≦π)]∫-∞xe-(x-u)*(x-u)/4σ*σdu=[1/√(2π)]∫-∞(x-u)/σe-Z*Z/2dz=φ[(x-u)/σ]由此可得,若X~N(u,σ*σ),則有P{x1xx≦≦1}=φ[(x2-u)/σ]-φ[(x1-u)/σ]由正態分布得對稱性,對Z~N(0,1),當Z<0將有φ(z)=∫-∞zφ(u)duφ(z)=∫z∞φ(u)du=1-φ(-z)例:設X~N(u,σ*σ),求P{u-kσ