外接球与内切球问题解题技巧梳理VIP免费

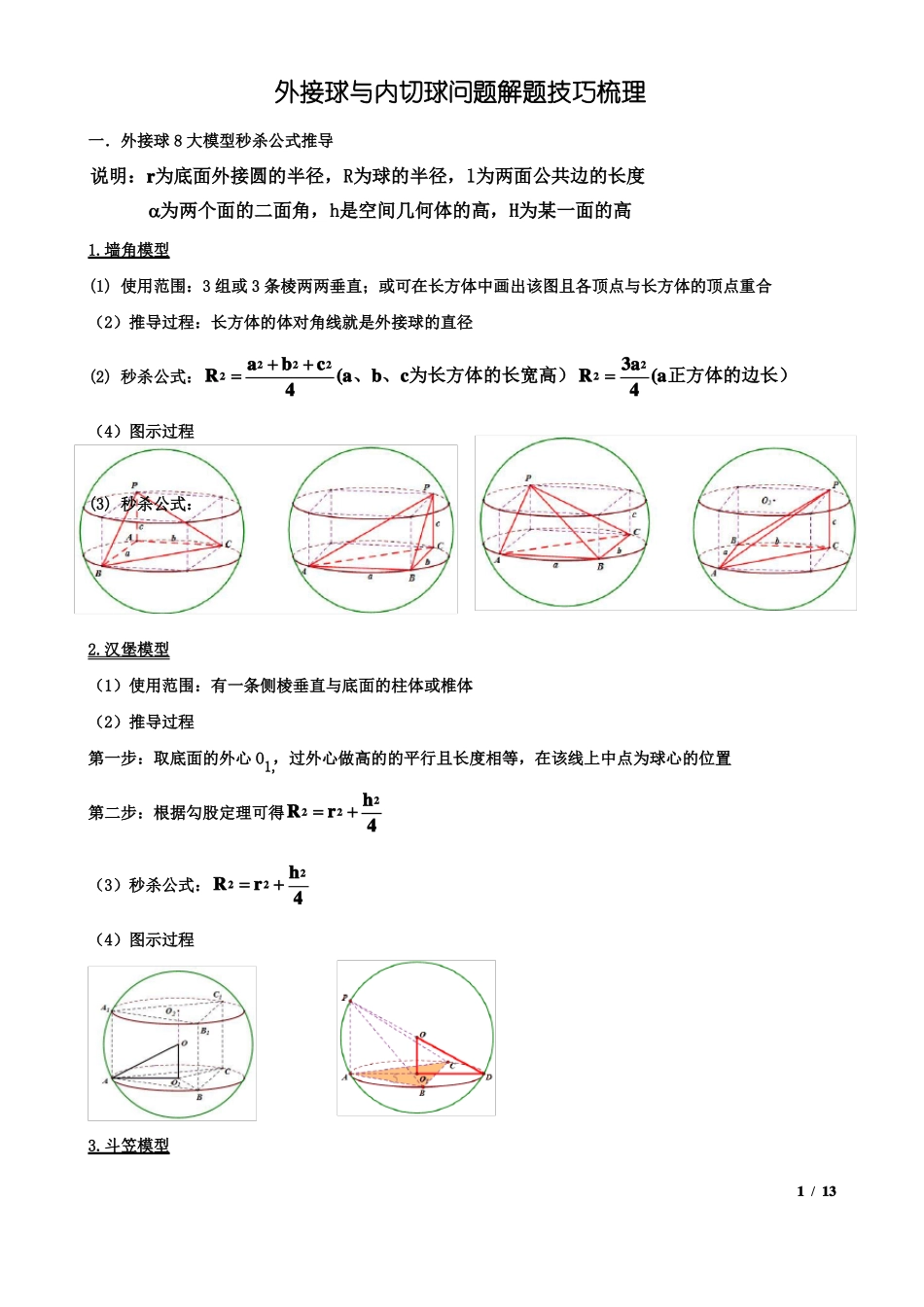
外接球与内切球问题解题技巧梳理一．外接球8大模型秒杀公式推导说明：r为底面外接圆的半径，R为球的半径，l为两面公共边的长度为两个面的二面角，h是空间几何体的高，H为某一面的高1.墙角模型(1)使用范围：3组或3条棱两两垂直；或可在长方体中画出该图且各顶点与长方体的顶点重合（2）推导过程：长方体的体对角线就是外接球的直径a2b2c23a22(2)秒杀公式：R(a、b、c为长方体的长宽高）R(a正方体的边长）442（4）图示过程(3)秒杀公式：2.汉堡模型（1）使用范围：有一条侧棱垂直与底面的柱体或椎体（2）推导过程第一步：取底面的外心O1,，过外心做高的的平行且长度相等，在该线上中点为球心的位置h2第二步：根据勾股定理可得Rr422h2（3）秒杀公式：Rr422（4）图示过程3.斗笠模型1/13（1）使用范围：正棱锥或顶点的投影在底面的外心上（2）推导过程第一步：取底面的外心O1,，连接顶点与外心，该线为空间几何体的高h第二步：在h上取一点作为球心Or2h2第三步：根据勾股定理R(hR)rR2h222r2h2（3）秒杀公式：R2h（4）图示过程4.折叠模型（1）使用范围：两个全等三角形或等腰三角形拼在一起，或菱形折叠（2）推导过程第一步：过两个平面取其外心H1、H2，分别过两个外心做这两个面的垂线且垂线相交于球心O=(CE-H1E)2tan2(Hr)2tan2(为两个平面的二面角）22222222r2第三步：OCOH1CH1(Hr)tan2222r2（3）秒杀技巧：R(Hr)tan2第二步：计算OH1H1Etan222（4）图示过程5.切瓜模型2/13（1）使用范围：有两个平面互相垂直的棱锥（2）推导过程：第一步：分别在两个互相垂直的平面上取外心F、N，过两个外心做两个垂面的垂线，两条垂线的交点即为球心O，取BC的中点为M，连接FM、MN、OF、ON第二步：l2ONMF为矩形由勾股可得OAANONANMFRrr2222222122（3）秒杀公式：R2r2r2l2124（4）图示过程6.麻花模型（1）使用范围：对棱相等的三棱锥（2）推导过程：设3组对棱的长度分别为x、y、z,长方体的长宽高分别为a、b、cx2a2b2ybcRx2y2z222228z2a2c2x2y2z2（3）秒杀公式：R28（4）图示过程43/137.矩形模型（1）使用范围：棱锥有两个平面为直角三角形且斜边为同一边（2）推导过程：根据球的定义可知一个点到各个顶点的距离相等该点为球心可得，斜边为球的直径3）秒杀公式：R2l2（4（4）图示过程8.鳄鱼模型（1）使用范围：适用所有的棱锥（2）推导过程：第一步：在两个平面上分别找外心O1、O2且过两外心做这两面的垂线相交于球心O第二步：O1OO2E四点共圆，正弦定理可得OE=2r=O1O2sin(1）在O2221O2E中，O1O2=O2EO1E2O2EO1Ecos（2）OD2O221OO1D（3）第三步：由（1）（2）（3)整理可得OD2O221OO1D=OE2O221EO1D2O1O222sin2O1EO1DOE2O221E2O2EO1Ecossin2O1E2O21DOE2O2=21E2O2EO1Ecossin2O221EO1B4/13第四步：设O2E=m，O1E=n，AB=l,两个面的二面角为m2n222mncosl2由第三步可得R=sin2+43）秒杀公式：R2=m2n22mncosl2（sin2+4（4）图示过程二．内切球的半径---等体积法1.推导过程以三棱锥P-ABC为例VPABC13S1111底面h3RSPAB3RSPAC3RSPBC3RSABC=13R(SPABSPACSPBCSABC)=13RS表面积R=3V几何体S表面积2.秒杀公式：R=3V几何体S表面积3.图示过程5/13技巧1外接球之墙角模型【例1】已知长方体ABCDA'B'C'D'中，A'B'3，B'C'1，A'B与平面ACC'A'所成角的正弦值为5，则该长方体的外接球的表面积为（）10A．4【举一反三】B．16C．163D．3231．棱长为2的正方体的外接球的表面积为（）A．4B．43C．12D．432．球面上有A,B,C,D四个点，若AB,AC,AD两两垂直，且ABACAD4，则该球的表面积为（）A．803B．32C．42D．48技巧2外接球之汉堡模型【例2】已知四棱锥ABCDE中，四边形BCDE是边长为2的正方形，AB3且AB平面BCDE，则该四棱锥外接球的表面积为（）A．4【举一反三】1．各顶点都在一个球面上的正四棱柱（底面是正方形，侧棱垂直于底面）高...