结构拓扑优化概述VIP免费

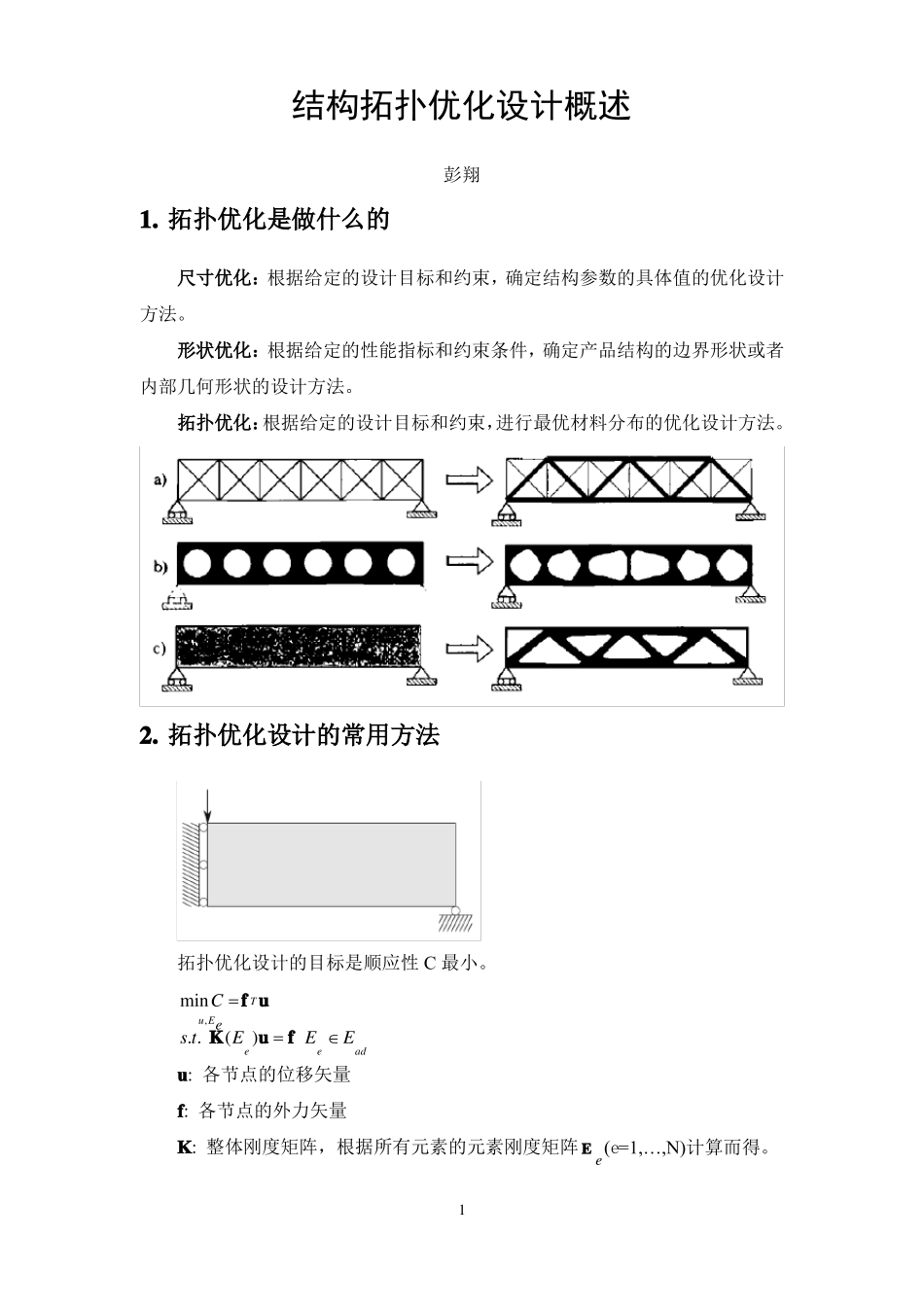
结构拓扑优化设计概述彭翔1.拓扑优化是做什么的尺寸优化：根据给定的设计目标和约束，确定结构参数的具体值的优化设计方法。形状优化：根据给定的性能指标和约束条件，确定产品结构的边界形状或者内部几何形状的设计方法。拓扑优化：根据给定的设计目标和约束，进行最优材料分布的优化设计方法。2.拓扑优化设计的常用方法拓扑优化设计的目标是顺应性C最小。minCfTuu,Ees.t.K(Ee)ufEeEadu:各节点的位移矢量f:各节点的外力矢量K:整体刚度矩阵，根据所有元素的元素刚度矩阵Ee(e=1,…,N)计算而得。1KKeEee1N2.1SIMP法(Simpleisotropicmaterialwithpenalization)将各元素点的材料分布问题看作为各点的密度值问题，将弹性模量设置为各点的密度值的函数，进行密度值分布优化设计。0弹性模量EijklxxpEijkl,p1xdV;0x1,x假设材料为各向同性的，将结构拓扑的变化转换为密度的变化，并使用罚因子p进行修正。0Eijkl00,Eijkl1Eijkl常用步骤：1)将设计域进行离散化，构建网格2)根据给定的体积比，确定各点的密度值为初始值xeVmaxVtotal3)根据各元素的密度值，确定元素刚度矩阵，进行设计目标(顺应性C)的计算。CEexeuTek0uee1NEexeEminxepE0Eminxe0,1xe为第e个元素的密度值；Eexe为第e个元素的弹性模量；Emin10-3其中，是一个无穷小量，表示空元素的弹性模量；E0为元素的弹性模量，p为系数，一般取为3。4)各元素点的敏感度计算。2目标函数的敏感度Cpxep1E0EminuTek0uexe总体积的敏感度V1xe为了避免“棋盘格”现象，过滤技术(Filter)被用于敏感度计算。目标函数的过滤性函数。ˆC1xemax,xeHeiiNeiNeHeixiCxiNe：与元素e的距离小于rmin的元素i的集合。Hei：权重系数，Heimax0,rmine,i。103：避免奇异性的无穷小数。设计变量的敏感度函数。~xeiNe1HeiiNeHeiix因此，过滤后的敏感度信息函数为：~C1CHje~xjeNjHeixeiNe5)更新策略CxeBeVxenewxemax0,xemifxeBemax0,xemmin1,xemifxeBemin1,xemxBotherwiseee6)收敛性分析。达到优化次数、两次迭代结果基本一致、设计目标误差小于给定值等，都可以作为收敛条件。3[1]推荐的书：《Topologyoptimization:Theoy,MethodsandApplications》[2]Sigmund,O.,A99linetopologyoptimizationcodewritteninMatlab.StructMultidiscOptim,2001.21:p.8.[3]ErikAndreassen,A.C.,MattiasSchevenels,BoyanS.Lazarov,OleSigmund,EfficienttopologyoptimizationinMATLABusing88linesofcode.StructMultidiscOptim,2011.43:p.16.2.2水平集法(LevelSetMethod)将结构边界看作为0水平集函数。通过构建高一维水平集函数，通过水平集函数的演化分析，进行结构边界的优化设计，获得满足要求的最优拓扑结构。k1xkxvxtt水平集方法的思路是：1）使用符号距离函数进行初始化，确定水平集边界和初始材料布局；2）构建目标函数Cx和约束函数VxVreq03）构建加权拉格朗日函数LxCxVxVreq1VxVreq224）计算每一节点的拓扑敏感度和元素敏感度5）根据拓扑敏感度和元素敏感度，确定每一节点处的水平集函数演化速度vx6）根据相邻节点的水平集值，计算水平集-元素的敏感度值in1intnminVin,0gDxi,DxinmaxVin,0gDxin,Dxin0niWithDxniin1inx,Dxinin1xgd,dmind,0maxd,0g-d,dmaxd,0mind,022227）计算每一节点处的，水平集函数-时间导数，确定第k+1个时刻的水平集函数k1xkxvxwgxtt48）确定k+1时刻的材料布局9）收敛性分析（迭代次数、两次材料布局差距等）[1]Challis,V.J.,Adiscretelevel-settopologyoptimizationcodewritteninMatl...