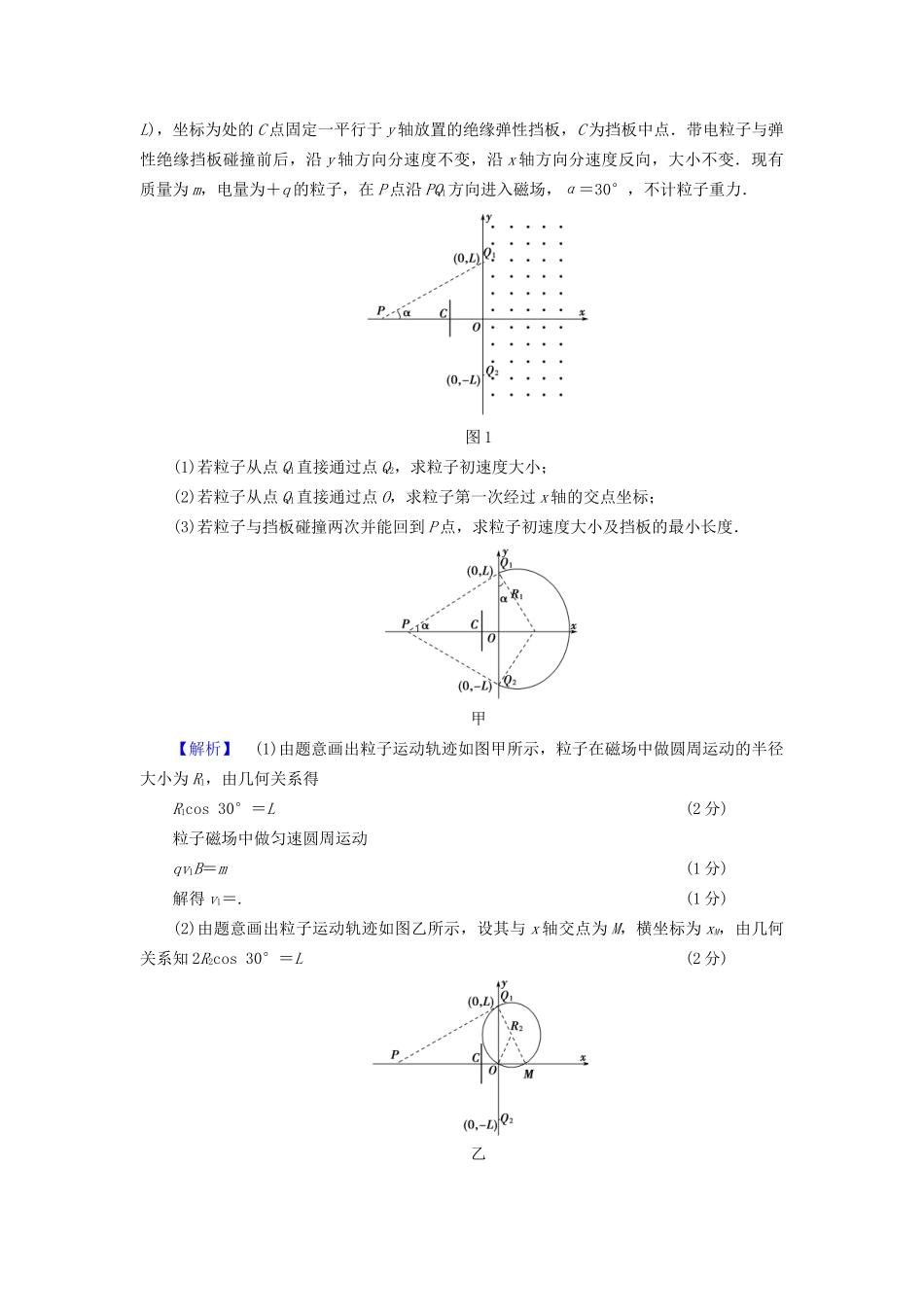
计算题32分强化练(三)1.(14分)在研究汽车的刹车性能时,让质量为2000kg的汽车在平直的公路上进行实验,在汽车车厢顶部悬挂一小球,并让汽车做匀速直线运动,小球相对汽车静止时悬线竖直,然后关闭发动机,发现小球与竖直方向的最大夹角为15°,若汽车在紧急制动时,发现小球与竖直方向的最大夹角为30°(tan15°=0.268,tan30°=0.577,g取10m/s2).(1)汽车紧急制动时的制动力为多大?(制动力是指由于刹车而增加的阻力,不包含运动过程中所受阻力)(2)若此汽车在高速公路上以90km/h的速度行驶,司机的反应时间为0.8s,该汽车行车时应保持的安全距离为多大?(结果取整数)【解析】(1)根据题意可得小球受力情况如图,由图可知,汽车关闭发动机时对小球由牛顿第二定律可得mgtan15°=ma1(2分)对汽车同理有f=Ma1(1分)汽车紧急制动时对小球由牛顿第二定律得mgtan30°=ma2(2分)设汽车紧急制动时的制动力为F,同理有F+f=Ma2(2分)联立可得F=6180N.(1分)(2)由(1)问可知a2=5.77m/s2(2分)由题可知v0=25m/s,t=0.8s在高速公路遇紧急情况停车的安全距离等于反应距离与刹车距离之和即有s=v0t+(2分)联立以上各式得s=74m.(2分)【答案】(1)6180N(2)74m2.(18分)如图1所示的xOy坐标系中,y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向外.Q1、Q2两点的坐标分别为(0,L)、(0,-L),坐标为处的C点固定一平行于y轴放置的绝缘弹性挡板,C为挡板中点.带电粒子与弹性绝缘挡板碰撞前后,沿y轴方向分速度不变,沿x轴方向分速度反向,大小不变.现有质量为m,电量为+q的粒子,在P点沿PQ1方向进入磁场,α=30°,不计粒子重力.图1(1)若粒子从点Q1直接通过点Q2,求粒子初速度大小;(2)若粒子从点Q1直接通过点O,求粒子第一次经过x轴的交点坐标;(3)若粒子与挡板碰撞两次并能回到P点,求粒子初速度大小及挡板的最小长度.甲【解析】(1)由题意画出粒子运动轨迹如图甲所示,粒子在磁场中做圆周运动的半径大小为R1,由几何关系得R1cos30°=L(2分)粒子磁场中做匀速圆周运动qv1B=m(1分)解得v1=.(1分)(2)由题意画出粒子运动轨迹如图乙所示,设其与x轴交点为M,横坐标为xM,由几何关系知2R2cos30°=L(2分)乙xM=2R2sin30°(1分)则M点坐标为.(1分)(3)由题意画出粒子运动轨迹如图丙所示,粒子在磁场中做圆周运动的半径大小为R3,偏转一次后在y负方向偏移量为Δy1,由几何关系得Δy1=2R3cos30°(1分)丙为保证粒子最终能回到P,粒子每次射出磁场时速度方向与PQ2连线平行,与挡板碰撞后,速度方向应与PQ1连线平行,每碰撞一次,粒子出进磁场在y轴上距离Δy2(如图中A、E间距)可由题给条件得Δy2=2tan30°(2分)当粒子只碰二次,其几何条件是3Δy1-2Δy2=2L(2分)解得R3=(1分)粒子磁场中做匀速圆周运动qv3B=m(1分)解得v3=(1分)挡板的最小长度ΔL=2R3cos30°-tan30°(1分)解得ΔL=.(1分)【答案】见解析