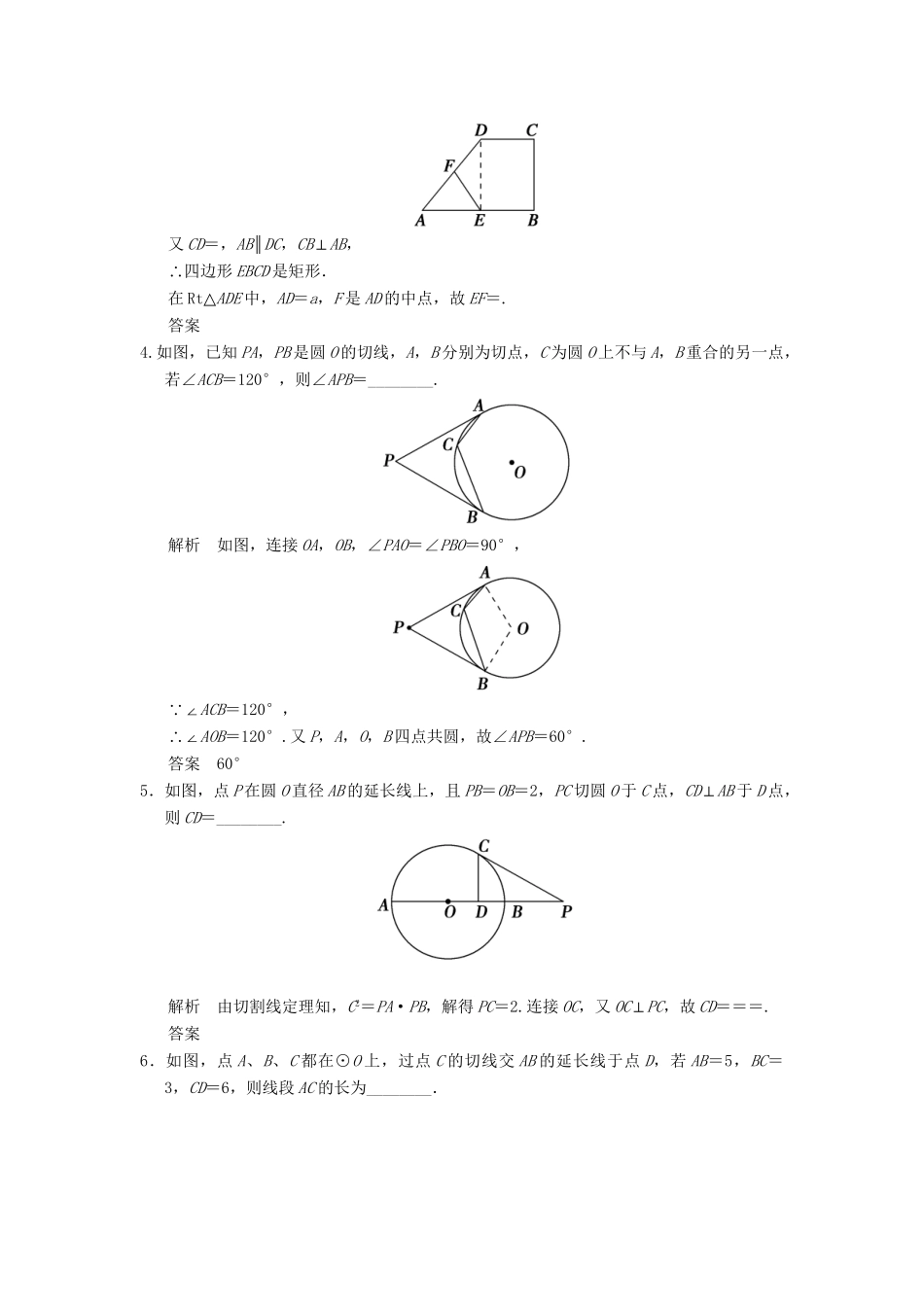
几何证明选讲A组(供高考题型为填空题的省份使用)1.如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=________.解析 AC=4,AD=12,∠ACD=90°,∴CD2=AD2-AC2=128,∴CD=8.又 AE⊥BC,∠B=∠D,∴△ABE∽△ADC,∴=,∴BE===4.答案42.如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为________.解析如图,连接CE,AO,AB.根据A,E是半圆周上的两个三等分点,BC为直径,可得∠CEB=90°,∠CBE=30°,∠AOB=60°,故△AOB为等边三角形,AD=,OD=BD=1,∴DF=,∴AF=AD-DF=.答案3.如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF=________.解析连接DE,由于E是AB的中点,故BE=.又CD=,AB∥DC,CB⊥AB,∴四边形EBCD是矩形.在Rt△ADE中,AD=a,F是AD的中点,故EF=.答案4.如图,已知PA,PB是圆O的切线,A,B分别为切点,C为圆O上不与A,B重合的另一点,若∠ACB=120°,则∠APB=________.解析如图,连接OA,OB,∠PAO=∠PBO=90°, ∠ACB=120°,∴∠AOB=120°.又P,A,O,B四点共圆,故∠APB=60°.答案60°5.如图,点P在圆O直径AB的延长线上,且PB=OB=2,PC切圆O于C点,CD⊥AB于D点,则CD=________.解析由切割线定理知,C2=PA·PB,解得PC=2.连接OC,又OC⊥PC,故CD===.答案6.如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为________.解析由切割线定理,得CD2=BD·AD.因为CD=6,AB=5,则36=BD(BD+5),即BD2+5BD-36=0,即(BD+9)(BD-4)=0,所以BD=4.因为∠A=∠BCD,所以△ADC∽△CDB,于是=.所以AC=·BC=×3=.答案7.如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为______.解析由题意,得弦切角∠BCD=∠A=60°,∠ACB=∠D=90°,∴△ABC∽△CBD.∴=,CD===5.又 CD与圆相切,∴CD2=DE·DB,则DE====5.答案58.如图,⊙O的割线PBA过圆心O,弦CD交PA于点F,且△COF∽△PDF,若PB=OA=2,则PF=________.解析由相交弦定理可得BF·AF=DF·CF,由△COF∽△PDF可得=,即得DF·CF=PF·OF.∴BF·AF=PF·OF,即(PF-2)·(6-PF)=PF·(4-PF),解得PF=3.答案39.如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若=,=,则的值为________.解析 ∠P=∠P,∠PCB=∠PAD,∴△PCB∽△PAD.∴==. =,=,∴=.答案10.如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=________.解析C为BD中点,且AC⊥BC,故△ABD为等腰三角形.AB=AD=6,∴AE=4,DE=2,又=⇒AC2=AE·AD=4×6=24,AC=2,在△ABC中,BC===2.答案211.如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD=________cm.解析如图,连接DC,则CD⊥AB,Rt△ADC∽Rt△ACB.故=,即=,AD=(cm),BD=5-=(cm).答案12.如图所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA.若AD=m,AC=n,则AB=________.解析 直线PB与圆相切于点B,且∠PBA=∠DBA,∴∠ACB=∠ABP=∠DBA,由此可得直线AB是△BCD外接圆的切线且B是切点,则由切割线定理得AB2=AD·AC=mn,即得AB=.答案13.如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF=,则线段CD的长为________.解析由相交弦定理得AF·FB=EF·FC,∴FC==2.由△AFC∽△ABD,可知=,∴BD==.由切割线定理得DB2=DC·DA,又DA=4CD,∴4DC2=DB2=,∴DC=.答案14.如图所示,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=,AF∶FB∶BE=4∶2∶1.若CE与圆相切,则线段CE的长为________.解析设AF=4k,BF=2k,BE=k,由DF·FC=AF·BF,得2=8k2,即k=.所以AF=2,BF=1,BE=,AE=.由切割线定理,得CE2=BE·EA...