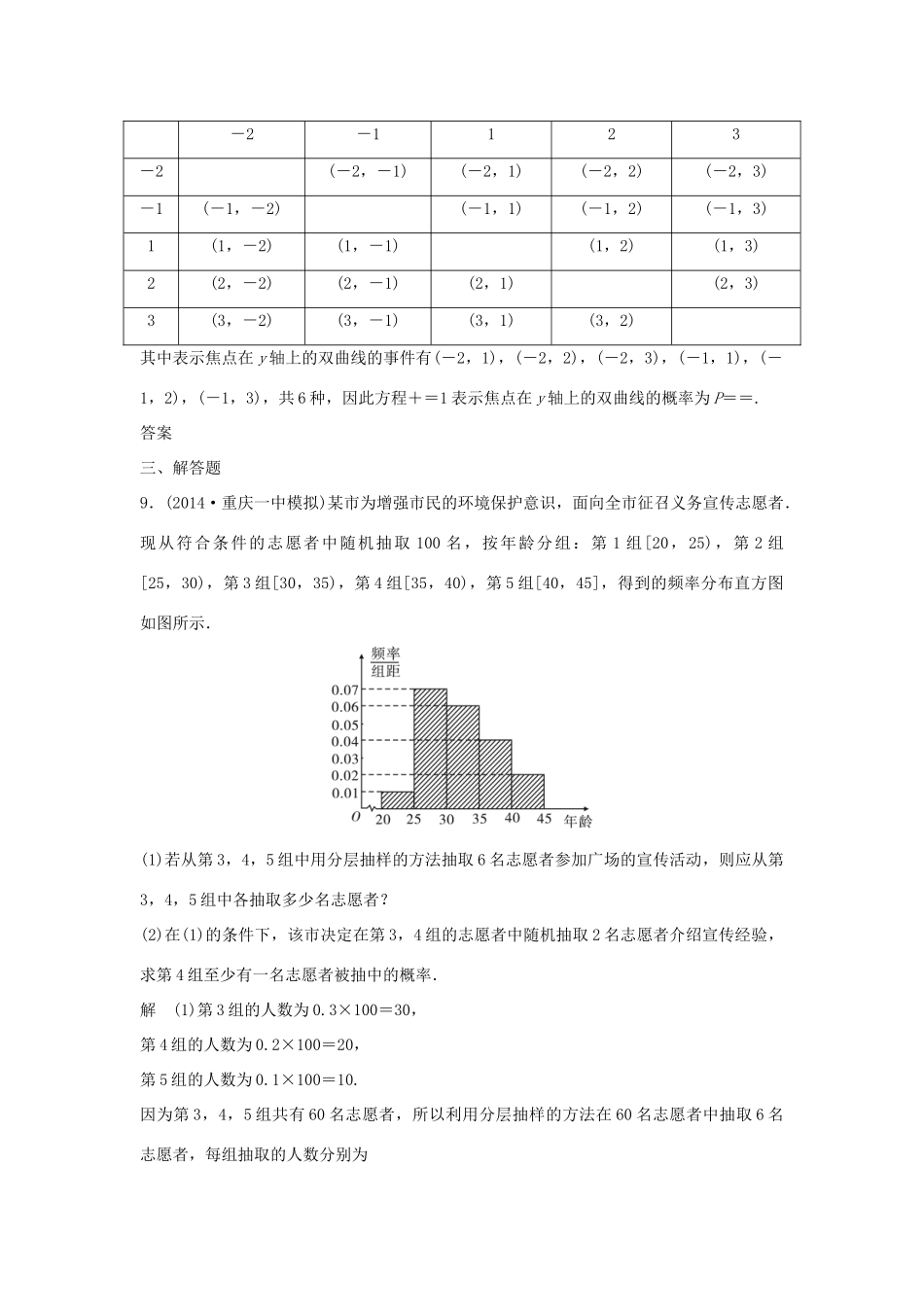
【大高考】(三年模拟一年创新)2016届高考数学复习第十章第二节古典概型与几何概型文(全国通用)A组专项基础测试三年模拟精选一、选择题1.(2015·云南名校统考)已知P是△ABC所在平面内一点,PB+PC+2PA=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是()A.B.C.D.解析取BC中点为D点. PB+PC=2PD=-2PA.∴点P为AD的中点,∴S△PBC=S△ABC,故黄豆落在△PBC内的概率为=.答案D2.(2014·湖南益阳模拟)在正六边形的6个顶点中随机选择4个顶点,则构成的四边形是梯形的概率为()A.B.C.D.解析如图,在正六边形ABCDEF的6个顶点中随机选择4个顶点,共有15种选法,其中构成的四边形是梯形的有ABEF、BCDE、ABCF、CDEF、ABCD、ADEF,共6种情况,故构成的四边形是梯形的概率P==,故选B.答案B二、填空题3.(2015·巴蜀中学一模)公共汽车在8:00到8:20内随机地到达某站,某人8:15到达该站,则他能等到公共汽车的概率为________.解析该人能等到公共汽车的概率为=.答案一年创新演练4.设a∈[0,10],则函数g(x)=在区间(0,+∞)内为增函数的概率为________.解析若函数g(x)=在区间(0,+∞)内为增函数,则a-2<0,∴a<2,又a∈[0,10],∴0≤a<2,故所求概率为=.答案5.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{0,1,2,3},若|a-b|≤1,则称甲、乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为()A.B.C.D.解析基本事件共有16种情况,而|a-b|≤1的情况共有10种,故所求概率为=.答案CB组专项提升测试三年模拟精选一、选择题6.(2015·北京西城区期末)某天,甲要去银行办理储蓄业务,已知银行的营业时间为9:00至17:00,设甲在当天13:00至18:00之间任何时间去银行的可能性相同,那么甲去银行恰好能办理业务的概率是()A.B.C.D.解析甲去银行恰好能办理业务的概率为=.答案D二、填空题7.(2014·广东惠州调研)投掷两颗相同的正方体骰子(骰子质地均匀,且各个面上依次标有点数1、2、3、4、5、6)一次,则两颗骰子向上点数之积等于12的概率为________.解析抛掷两颗骰子的基本事件总数为6×6=36,两颗骰子向上点数之积为12的基本事件有(2,6),(3,4),(4,3),(6,2),共4种,故所求概率为=.答案8.(2014·长沙二模)若实数m、n∈{-2,-1,1,2,3},且m≠n,则方程+=1表示焦点在y轴上的双曲线的概率是________.解析实数m、n满足m≠n的基本事件有20种,如下表所示.-2-1123-2(-2,-1)(-2,1)(-2,2)(-2,3)-1(-1,-2)(-1,1)(-1,2)(-1,3)1(1,-2)(1,-1)(1,2)(1,3)2(2,-2)(2,-1)(2,1)(2,3)3(3,-2)(3,-1)(3,1)(3,2)其中表示焦点在y轴上的双曲线的事件有(-2,1),(-2,2),(-2,3),(-1,1),(-1,2),(-1,3),共6种,因此方程+=1表示焦点在y轴上的双曲线的概率为P==.答案三、解答题9.(2014·重庆一中模拟)某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名,按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,则应从第3,4,5组中各抽取多少名志愿者?(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.解(1)第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10.因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为第3组:×6=3;第4组:×6=2;第5组:×6=1.所以应从第3,4,5组中分别抽取3人,2人,1人.(2)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,则从5名志愿者中抽取2名志愿者有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共10种.其中第4组的2名志愿者B1,B2至少...