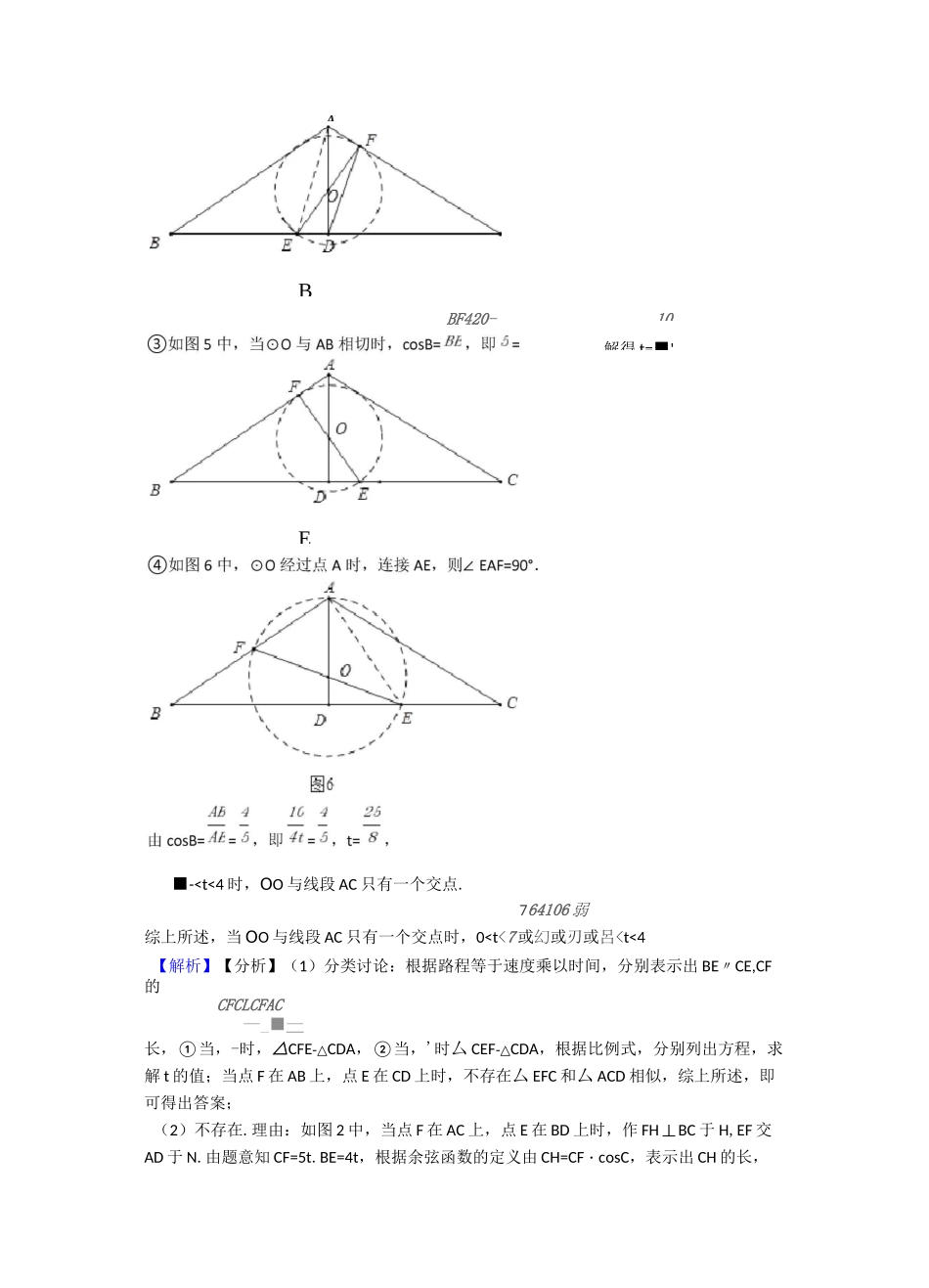
一、相似真题与模拟题分类汇编(难题易错题)1.如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD丄BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).(1)求x为何值时,△EFC和厶ACD相似;(2)是否存在某一时刻,使得△EFD被AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.答案】(1)解:如图1中,CFCL二点F在AC上,点E在BD上时,①当--时,△CFE-△CDA,5t8•••口一陽=.-,64t=',•t=2,当点F在AB上,点E在CD上时,不存在厶EFC和厶ACD相似,64综上所述,t='s或2s时,△EFC和厶ACD相似.(2)解:不存在.理由:如图2中,当点F在AC上,点E在BD上时,作FH丄BC于H,EF交AD于N.TCF=5t.BE=4t,CH=CF・cosC=4t,BE=CH,TAB=AC,AD丄BC,.BD=DC,.DE=DH,TDNIIFH,ED.■'/=1,.EN=FN,'△END=SAFND.△EFD被AD分得的两部分面积相等,同法可证当点F在AB上,点E在CD上时,△EFD被AD分得的两部分面积相等,•••不存在某一时刻,使得△EFD被AD分得的两部分面积之比为3:5.(3)解:①如图3中,当以EF为直径的O0经过点A时,OO与线段AC有两个交点,•t=-,7•••0