高三数学（理）第一轮复习：平面与空间直线；直线与平面平行；平面与平面平行人教版VIP免费

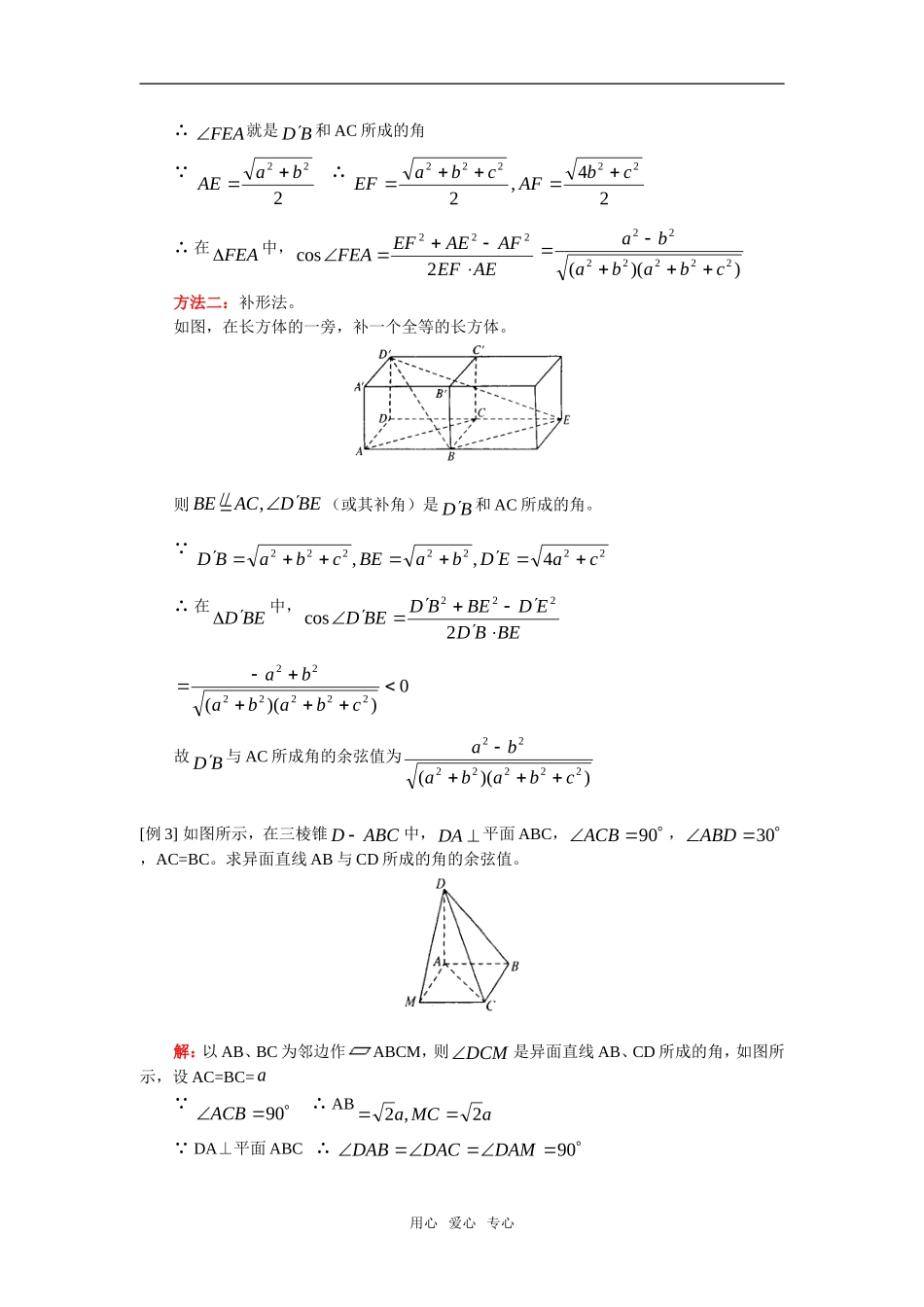
高三数学（理）第一轮复习：平面与空间直线；直线与平面平行；平面与平面平行人教版【本讲教育信息】一.教学内容：平面与空间直线；直线与平面平行；平面与平面平行二.本周教学重、难点：1.掌握平面的基本性质，两条直线平行与垂直的判定和性质定理，两条直线所成的角和距离的概念。2.掌握直线与平面平行、平面与平面平行的判定定理和性质定理；直线和平面的距离；平面和平面间的距离的概念。【典型例题】[例1]有空间不同的五个点。（1）若有某四点共面，则这五点最多可确定多少个平面？（2）若任意四点都在同一平面内，则这五点共能确定多少个平面？并证明你的结论。解：（1）当共面的某四点不共线，另一点不在该平面内时，这五点确定的平面最多，如图，最多可确定7个平面。（2）若任意四点都在同一平面内时，这五点必共面，证明如下：若A、B、C、D四点在内，又 A、B、C、P在同一平面内，可分如下情况证明：①若A、B、C三点不共线，则为A、B、C确定的平面，∴P在内，五点共面；②若A、B、C三点在直线l上，则<1>当D或P也在l上时，五点共面；<2>若D、P都不在l上，则DP直线与AB直线必在A、B、D、P所在的平面上，∴C也在这一平面内，从而五点也共面。[例2]已知长方体DCBAABCD中，AB=)(,,bacAAbBCa，求异面直线BD和AC所成角的余弦。解析：方法一：平移法。如图，连结BD交AC于E，取DD的中点F，连结EF，则BDEF21//用心爱心专心∴FEA就是BD和AC所成的角 22baAE∴24,222222cbAFcbaEF∴在FEA中，AEEFAFAEEFFEA2cos222))((2222222cbababa方法二：补形法。如图，在长方体的一旁，补一个全等的长方体。则BEDACBE,//（或其补角）是BD和AC所成的角。 22222224,,caEDbaBEcbaBD∴在BED中，BEBDEDBEBDBED2cos2220))((2222222cbababa故BD与AC所成角的余弦值为))((2222222cbababa[例3]如图所示，在三棱锥ABCD中，DA平面ABC，90ACB，30ABD，AC=BC。求异面直线AB与CD所成的角的余弦值。解：以AB、BC为邻边作ABCM，则DCM是异面直线AB、CD所成的角，如图所示，设AC=BC=a 90ACB∴ABaMCa2,2 DA⊥平面ABC∴90DAMDACDAB用心爱心专心 30ABD∴aDA36又AM=a∴DM=DC=a315∴10302cos222MCDCDMMCDCDCM[例4]如图，已知正方形ABCD，边长为1，过D作PD⊥平面ABCD，且PD=1，E、F分别是AB和BC的中点。（1）求D点到平面PEF的距离；（2）求直线AC到平面PEF的距离。解：（1）方法一：因为EF⊥BD，EF⊥PD，所以EF⊥平面PDB所以平面PEF⊥平面PDB，交线为PG所以D点到平面PEF的距离，就是D到PG的距离h在PDG中，PGDGPDh，而243,1DGPD43416181PG，所以171734342431h就是D到平面PEF的距离。方法二：因为DEFPPEFDVV，即PDShSDEFPEF3131所以1717343422211)2432221(PEFDEFSPDSh所以D到平面PEF的距离是17173（2）连结AC交BD于O，则O到平面PEF的距离就为所求，因为平面PDG⊥平面PEF，所以O到PG的距离就是O到平面的距离，如图所示在PDGRt中，OH⊥PG，所以OHGPDG~所以241,1,OGPDOGPGOHPD用心爱心专心434)243(12PG所以17171714342411OH所以AC到平面PEF的距离是1717[例5]如图，已知正方体DCBAABCD中，面对角线BA、CB上分别有两点E、F且EB=FC。求证：（1）EF//平面ABCD；（2）平面//DAC平面CBA证明：（1）证法一：过E、F分别作AB、BC的垂线EM、FN分别交AB、BC于M、N连结MN， BB平面ABCD∴BCBBABBB,∴BBFNBBEM//,//∴FNEM// FCEBCBBA,∴AE=BF又45BCCABB BNFRtAMERt∴EM=FN∴四边形MNFE是平行四边形∴EF//MN又MN平面ABCD∴EF//平面ABCD证法二：过E作EG//AB交BB于G，连结GF∴BBGBABEB BCABFCEB,∴BBGBBCFC∴BCCBFG////又 BBCABGFGEG,∴平面EFG//平面ABCD又EF平面EFG∴EF//平面ABCD用心爱...