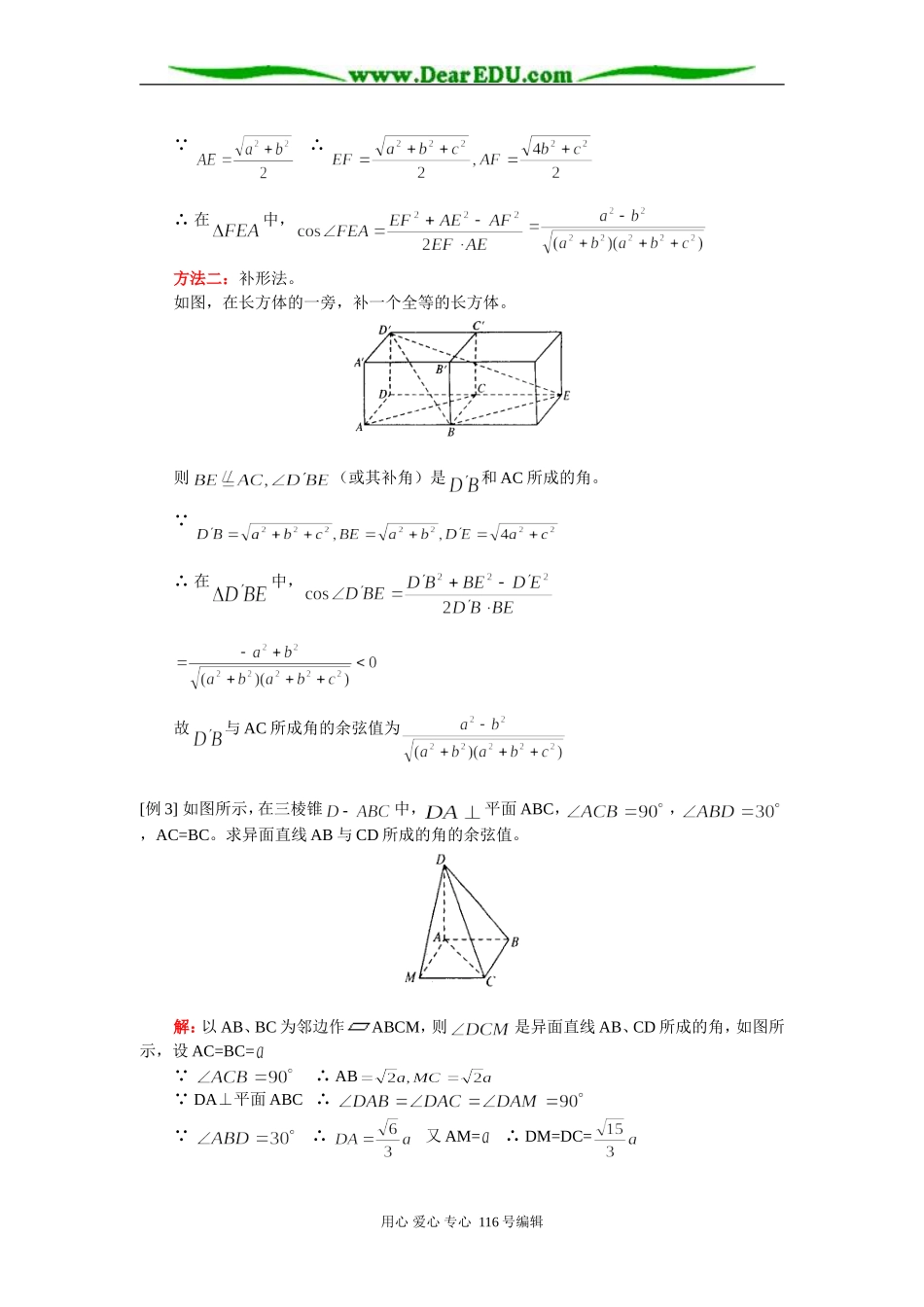
高三数学(理)平面与空间直线;直线与平面平行;平面与平面平行知识精讲人教版【本讲教育信息】一.教学内容:平面与空间直线;直线与平面平行;平面与平面平行二.本周教学重、难点:1.掌握平面的基本性质,两条直线平行与垂直的判定和性质定理,两条直线所成的角和距离的概念。2.掌握直线与平面平行、平面与平面平行的判定定理和性质定理;直线和平面的距离;平面和平面间的距离的概念。【典型例题】[例1]有空间不同的五个点。(1)若有某四点共面,则这五点最多可确定多少个平面?(2)若任意四点都在同一平面内,则这五点共能确定多少个平面?并证明你的结论。解:(1)当共面的某四点不共线,另一点不在该平面内时,这五点确定的平面最多,如图,最多可确定7个平面。(2)若任意四点都在同一平面内时,这五点必共面,证明如下:若A、B、C、D四点在内,又 A、B、C、P在同一平面内,可分如下情况证明:①若A、B、C三点不共线,则为A、B、C确定的平面,∴P在内,五点共面;②若A、B、C三点在直线上,则<1>当D或P也在上时,五点共面;<2>若D、P都不在上,则DP直线与AB直线必在A、B、D、P所在的平面上,∴C也在这一平面内,从而五点也共面。[例2]已知长方体中,AB=,求异面直线和AC所成角的余弦。解析:方法一:平移法。如图,连结BD交AC于E,取的中点F,连结EF,则∴就是和AC所成的角用心爱心专心116号编辑 ∴∴在中,方法二:补形法。如图,在长方体的一旁,补一个全等的长方体。则(或其补角)是和AC所成的角。 ∴在中,故与AC所成角的余弦值为[例3]如图所示,在三棱锥中,平面ABC,,,AC=BC。求异面直线AB与CD所成的角的余弦值。解:以AB、BC为邻边作ABCM,则是异面直线AB、CD所成的角,如图所示,设AC=BC= ∴AB DA⊥平面ABC∴ ∴又AM=∴DM=DC=用心爱心专心116号编辑∴[例4]如图,已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=1,E、F分别是AB和BC的中点。(1)求D点到平面PEF的距离;(2)求直线AC到平面PEF的距离。解:(1)方法一:因为EF⊥BD,EF⊥PD,所以EF⊥平面PDB所以平面PEF⊥平面PDB,交线为PG所以D点到平面PEF的距离,就是D到PG的距离在中,,而,所以就是D到平面PEF的距离。方法二:因为,即所以所以D到平面PEF的距离是(2)连结AC交BD于O,则O到平面PEF的距离就为所求,因为平面PDG⊥平面PEF,所以O到PG的距离就是O到平面的距离,如图所示在中,OH⊥PG,所以所以所以所以AC到平面PEF的距离是用心爱心专心116号编辑[例5]如图,已知正方体中,面对角线、上分别有两点E、F且=。求证:(1)EF//平面ABCD;(2)平面平面证明:(1)证法一:过E、F分别作AB、BC的垂线EM、FN分别交AB、BC于M、N连结MN, 平面ABCD∴∴∴ ∴AE=BF又 ∴EM=FN∴四边形MNFE是平行四边形∴EF//MN又平面ABCD∴EF//平面ABCD证法二:过E作EG//AB交于G,连结GF∴ ∴∴又 ∴平面EFG//平面ABCD又平面EFG∴EF//平面ABCD(2)证法一:如图所示,正方体中,又=∴平面平面证法二:连结 平面,∴(三垂线定理)同理,,又∴平面同理,平面∴平面平面用心爱心专心116号编辑[例6]如图所示,是边长为的正方形纸片,是正三角形,若去掉,分别以BD、CD为棱将面ABD,翻折,使A和重合,构成四面体形状,如图所示,求四面体ABCD中A点到平面BCD的距离。解: 为等边三角形∴∴ AB=AC=BC∴与都是等边三角形取BC的中点E,连结AE、DE,则BC⊥AE,BC⊥DE∴BC⊥截面ADE∴底面BCD⊥截面ADE过A作AF⊥DE于F,则AF⊥底面BCD在中,∴∴故A到平面BCD的距离为AF=AE[例7]如图所示,在四棱锥中,底面四边形ABCD是边长为4的菱形,并且,VA=3,VA⊥底面ABCD,O是AC、BD的交点,OE⊥VC于E。求:(1)点V到CD的距离;(2)异面直线VC与BD的距离;(3)点B到平面VCD的距离。用心爱心专心116号编辑解:(1)由已知∴∴是正三角形,取CD的中点F,连结AF、VF,则CD⊥AF又VA⊥面ABCD∴CD⊥VF(三垂线定理)∴VF为点V到CD的距离 AD=4∴AF=(2) 底面四边形ABCD是菱形∴BD⊥AC又VA⊥底面ABCD∴VA⊥BD∴BD⊥面VAC∴BD⊥OE由已知OE⊥VC∴OE是异面直线BD和VC的公垂线段由(1)可知 ∴∴(3) AB//CD∴AB//面VCD,点B到...