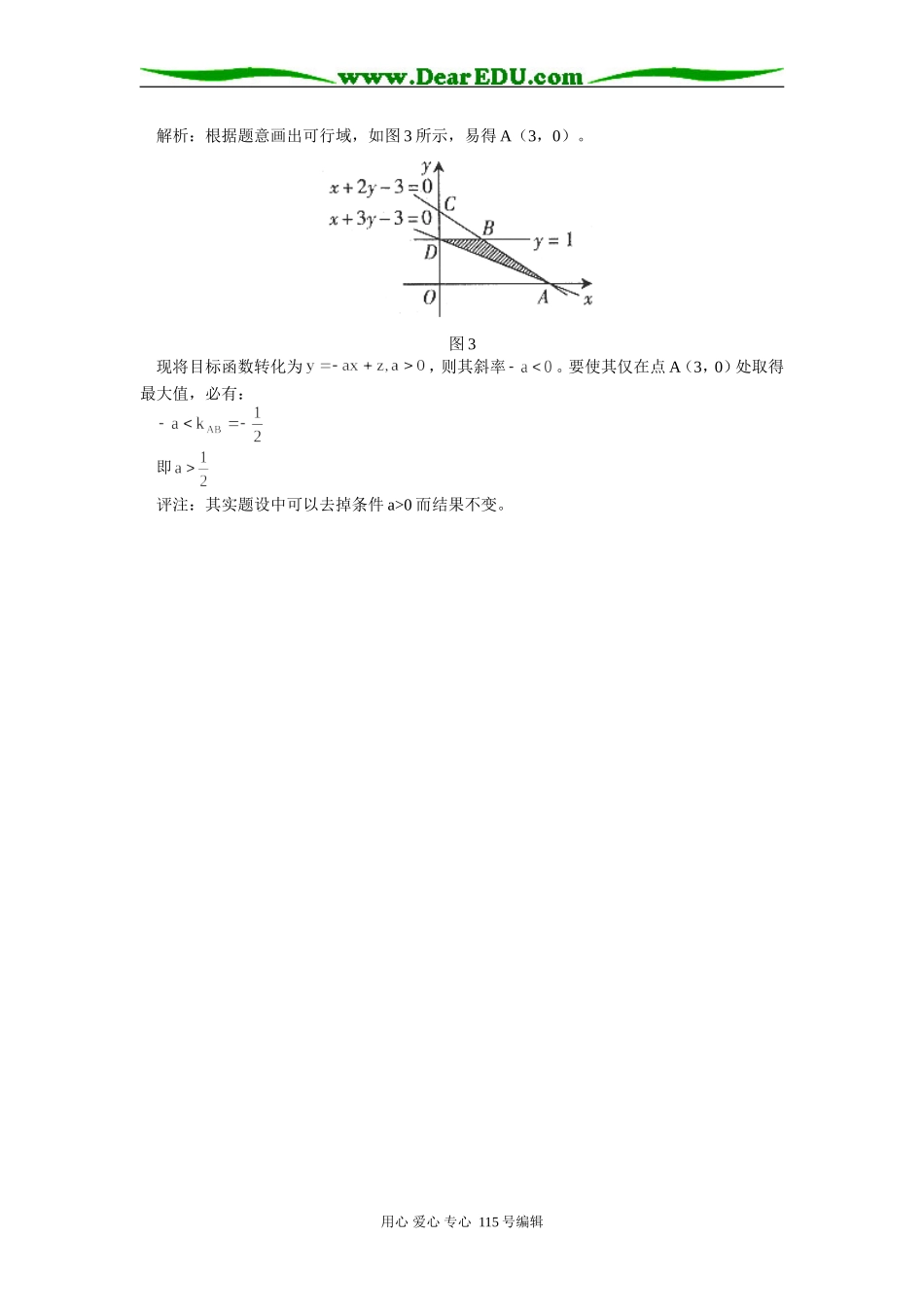
高三数学线性规划中参数的探讨在解决线性规划问题时,约束条件和目标函数中常涉及到一些参数,这些参数需通过最值问题加以求解。下面举例说明,供同学们学习时参考。一、约束条件中的参数例1.线性目标函数在线性约束条件下取得最大值的最优解只有一个,则实数a的取值范围为___________________。解析:根据题意,画出可行域,如图1所示,可求得A(1,2),将目标函数变形为,与边界线平行,而要使最大值的最优解只有一个,则分析图形知可行域只能为直线y=2下方的部分(含边界线),故实数a的取值范围为。图1评注:运用数形结合思想,通过比较有关直线的倾斜程度而直观求解。二、目标函数中的参数1.最优解无穷求参数值例2.已知三点A(5,2),B(1,1),C(3,4),平面区域为△ABC的内部及边界,若使目标函数z=ax+y取得最大值的最优解有无数多个,求实数a的值。解析:画出符合题意的图形,如图2所示,将目标函数转化为。则若使目标函数取得最大值的最优解有无数多个,必有,或,即。图2评注:若最优解有无穷多个,说明目标函数和斜率等于某一边界线的斜率,则由此列出方程而求出某系数的具体数值。2.最优解唯一求参数范围例3.已知变量x,y满足,若目标函数(其中a>0)仅在点(3,0)处取得最大值,则a的取值范围为_______________。用心爱心专心115号编辑解析:根据题意画出可行域,如图3所示,易得A(3,0)。图3现将目标函数转化为,则其斜率。要使其仅在点A(3,0)处取得最大值,必有:即评注:其实题设中可以去掉条件a>0而结果不变。用心爱心专心115号编辑