高三数学立体几何综合训练（文）人教实验版（A）VIP免费

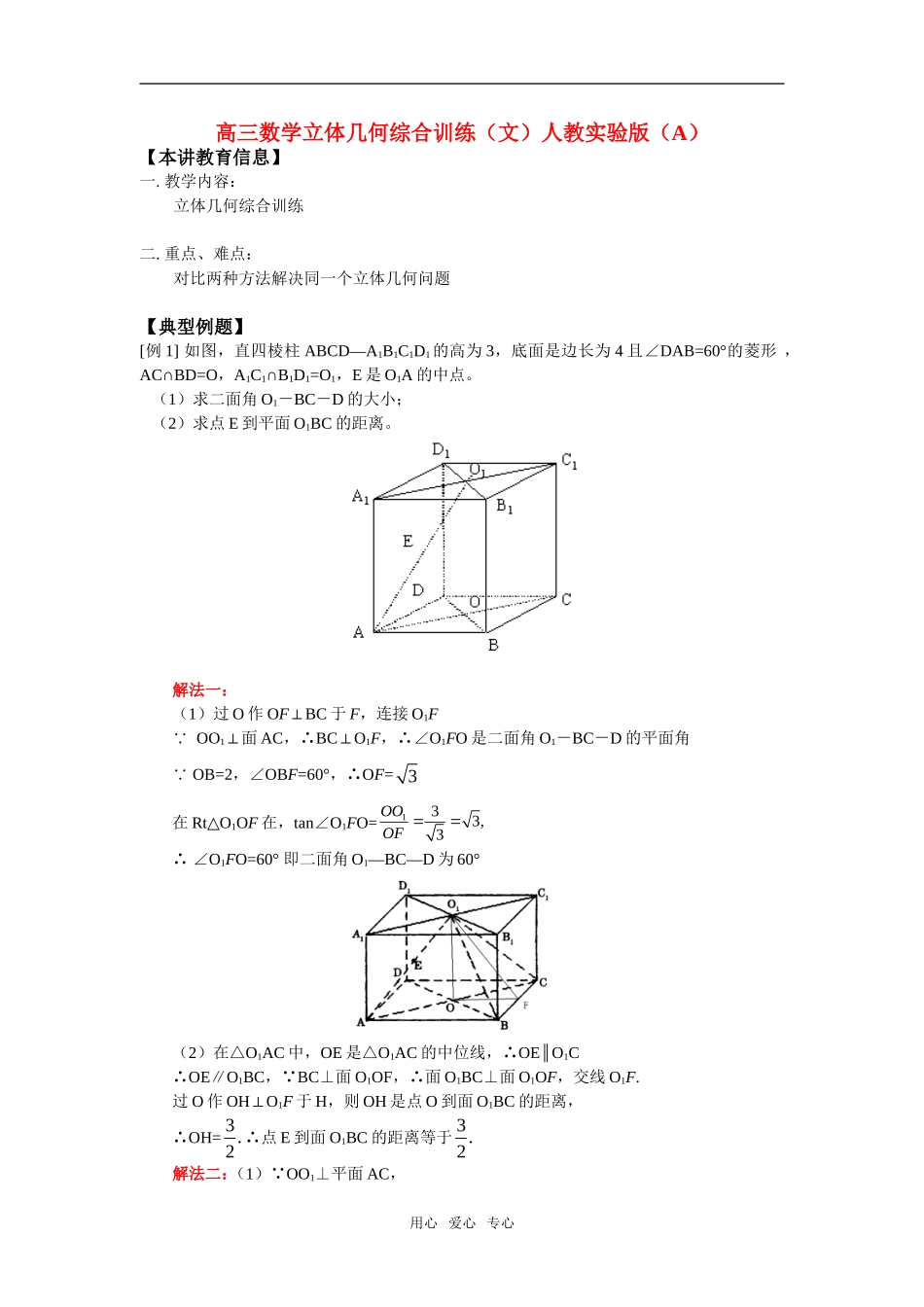
高三数学立体几何综合训练（文）人教实验版（A）【本讲教育信息】一.教学内容：立体几何综合训练二.重点、难点：对比两种方法解决同一个立体几何问题【典型例题】[例1]如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠DAB=60°的菱形，AC∩BD=O，A1C1∩B1D1=O1，E是O1A的中点。（1）求二面角O1－BC－D的大小；（2）求点E到平面O1BC的距离。解法一：（1）过O作OFBC⊥于F，连接O1F OO1⊥面AC，∴BCO⊥1F，∴∠O1FO是二面角O1－BC－D的平面角 OB=2，∠OBF=60°，∴OF=3在RtO△1OF在，tanO∠1FO=133,3OOOF∴O∠1FO=60°即二面角O1—BC—D为60°（2）在△O1AC中，OE是△O1AC的中位线，∴OEO∥1COEO∴∥1BC， BC⊥面O1OF，∴面O1BC⊥面O1OF，交线O1F.过O作OHO⊥1F于H，则OH是点O到面O1BC的距离，OH=∴3.2∴点E到面O1BC的距离等于3.2解法二：（1） OO1⊥平面AC，用心爱心专心OO∴1OA⊥，OO1OB⊥，又OAOB⊥，建立如图所示的空间直角坐标系（如图） 底面ABCD是边长为4，∠DAB=60°的菱形，OA=∴23，OB=2，则A（23，0，0），B（0，2，0），C（－23，0，0），O1（0，0，3）设平面O1BC的法向量为1n�=（x，y，z），则1n�⊥1OB�，1n�⊥1OC�，∴2302330yzxz，则z=2，则x=－3，y=3，∴1n�=（－3，3，2），而平面AC的法向量2n�=（0，0，3）cos<∴1n�，2n�>=21436||||2121nnnn，设O1－BC－D的平面角为α，∴cosα=1,2α=60°.∴故二面角O1－BC－D为60°（2）设点E到平面O1BC的距离为d， E是O1A的中点，∴1EO�=（－3，0，32），则d=2323)3(|)2,3,3()23,0,3(|||||22211nnEO∴点E到面O1BC的距离等于32。[例2]如图，在长方体ABCD—A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动。（1）证明：D1E⊥A1D；（2）当E为AB的中点时，求点A到面ECD1的距离；（3）AE等于何值时，二面角D1—EC—D的大小为4。用心爱心专心（1）证明：连1AD，在长方体ABCD—A1B1C1D1中，1AD为1DE在平面1AD的射影，而AD=AA1=1，则四边形11ADDA是正方形11ADAD，由三垂线定理得D1E⊥A1D（2）解：以点D为原点，DA为x轴，DC为y轴建立如图所示的直角坐标系。则(1,0,0)A(1,1,0)E、(1,2,0)B、(0,2,0)C、1(0,0,1)D则(0,1,0)AE�，(1,1,0)EC�，1(0,2,1)DC�，设平面1DEC的法向量为1(,,)nxyz�∴11100::1:1:2200nECxyxyzyznDC��，记1(1,1,2)n�∴点A到面ECD1的距离11||166||6AEndn��（3）解：设0(1,,0)Ey则0(1,2,0)ECy�，设平面1DEC的法向量为1(,,)nxyz�∴100110(2)0::(2):1:2200nECxyyxyzyyznDC��，记10((2),1,2)ny�而平面ECD的法向量2(0,0,1)n�，则二面角D1—EC—D的平面角12,4nn�∴12022212022cos232||||(2)121nnynny��∴当AE=23时，二面角D1—EC—D的大小为4。[例3]在四棱锥P—ABCD中，底面ABCD是a的正方形，PA⊥平面ABCD，且PA=2AB（1）求证：平面PAC⊥平面PBD；（2）求二面角B—PC—D的余弦值。用心爱心专心解：（1）证明： PA⊥平面ABCDPABD∴⊥ ABCD为正方形∴ACBD⊥∴BD⊥平面PAC又BD在平面BPD内，∴平面PAC⊥平面BPD（2）解法一：在平面BCP内作BNPC⊥垂足为N，连DN， RtPBCRtPDC△△≌，由BNPC⊥得DNPC⊥；∴BND∠为二面角B—PC—D的平面角，在△BND中，BN=DN=a65，BD=a2∴cosBND=∠5135265652222aaaa解法二：以A为原点，AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间坐标系如图，在平面BCP内作BNPC⊥垂足为N连DN， RtPBCRtPDC△△≌，由BNPC⊥得DNPC⊥；∴BND∠为二面角B—PC—D的平面角设)2,,(aaaPCPN650)2)(22()()(0)2,,()22,,(aaaaaaaaPCBNPCBNaaaPCaaaaaPBPNBN即用心爱心专心)3,6,65(),3,65,6(aaaNDaaaNB5136309365365||||cos2222aaaaNDNBNDNBBND解法三：以A为原点，AB、AD、AP所在直线分别为x轴、y轴、z轴建立如图空间坐标系...