高三数学立体几何（二）人教实验版（A）知识精讲VIP专享VIP免费

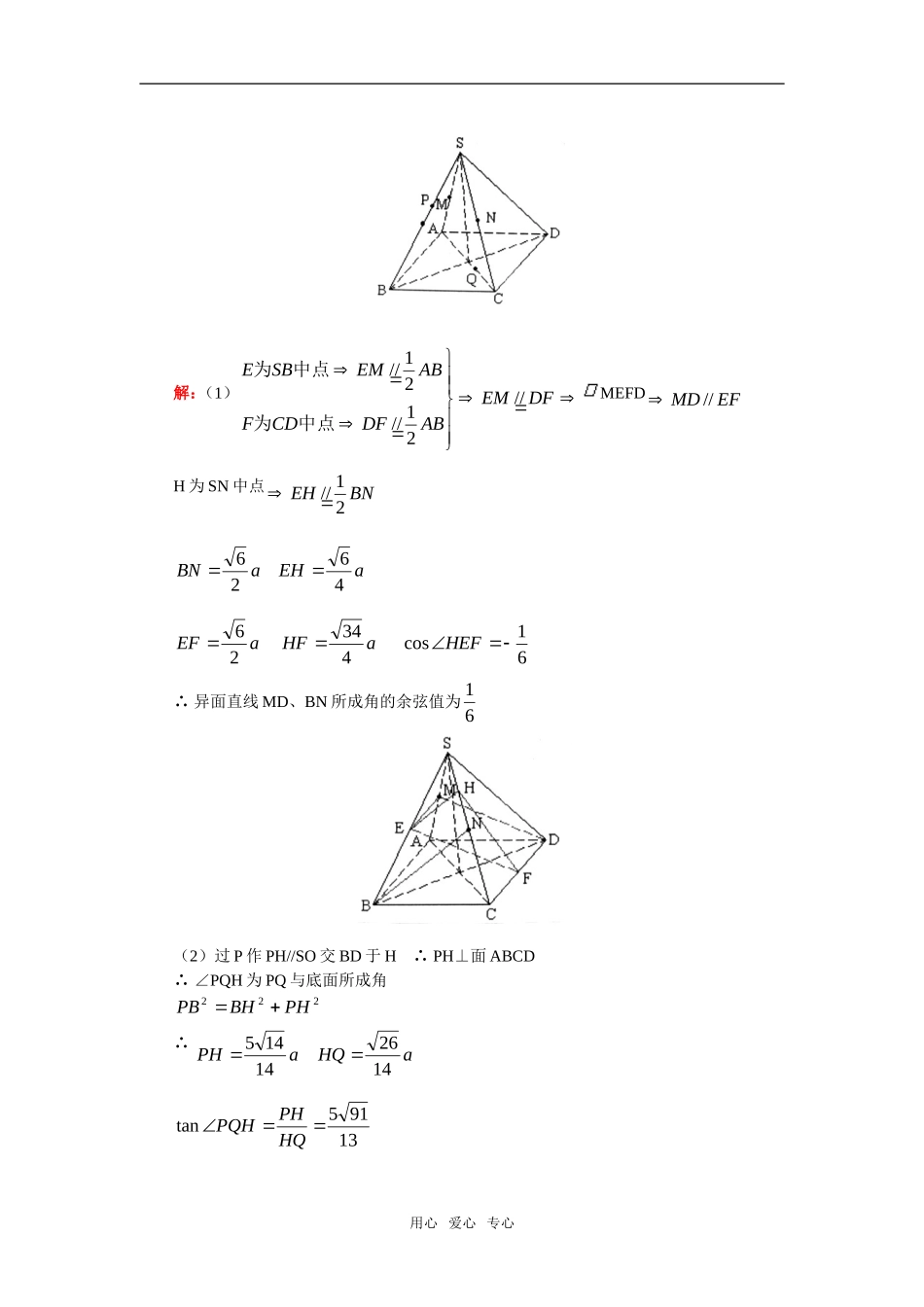
高三数学立体几何（二）人教实验版（A）【本讲教育信息】一.教学内容：立体几何（二）二.重点、难点：1.角度（1）两条异面直线所成角]2,0(（2）直线与平面所成角]2,0[（3）二面角],0[2.距离（1）作垂线（2）体积转化【典型例题】[例1]PA、PB、PC两两垂直，l与PA、PB所成角为45°，60°，求l与PC所成角。解：构造长方体1coscoscos2221cos4121221cos60[例2]正四棱锥S—ABCD中，AB=a，SA=a2，M为SA中点，N为SC中点。（1）求BN，DM所成角的余弦值；（2）P、Q在SB、CA上，5:2::QACQPBSP，求PQ与底面ABCD所成角的正切值。用心爱心专心解：（1）DFEMABDFCDFABEMSBE//21//21//中点为中点为MEFDEFMD//H为SN中点BNEH21//aBN26aEH4661cos43426HEFaHFaEF∴异面直线MD、BN所成角的余弦值为61（2）过P作PH//SO交BD于H∴PH⊥面ABCD∴∠PQH为PQ与底面所成角222PHBHPB∴aPH14145aHQ142613915tanHQPHPQH用心爱心专心[例3]SA⊥面ABC，AB⊥BC，DE在面SAC内，垂直平分SC，交SC、AC于E、D，若SA=AB=1，BC=2，求二面角（1）B—SC—A的余弦值；（2）E—BD—C。解：（1）SCSCDESCBEBCSBABSA221面DEB∴∠DEB为二面角A—SC—B的平面角BDBDSADBSCBEDSC面面SAC∴∠EDC为二面角C—BD—E的平面角∴BEDEDEBcosCDDEEDCcos AB=SA=1AC=3SC=2∴BE=1DE=33CD=332∴33cosDEB 21cosCDDEEDC∴60EDC用心爱心专心[例4]正方体ABCD—A1B1C1D1中，AB=1，求：（1）D到面D1AC的距离；（2）C到面AB1D1的距离；（3）M为BB1中点，M到面D1AC的距离；（4）AC1与BB1的距离解：（1）连BD∩AC=EBBDDACACDDBDAC111面过D作DF⊥D1E于F，ACDDFEDDFDFAC11面∴DF为距离33DF（2）设C到面AB1D1的距离为h∴hSVDABDABC111131用心爱心专心hV]60sin)2(21[31312正332h（3）连DM交D1E于H，设M到面D1AC距离为hhDFHMDH3221HMDHDHMG∴23h（4）),(),(11111AACCBBdBBACd面22,11BEAACCBd面[例5]四棱锥P—ABCD，底面ABCD为菱形，AB=2，∠BAD=60°，PB=PD，PA=PC=6，求：（1）B到面PAD的距离；（2）BC与PA的距离；（3）AC与PD的距离。解：（1）AC∩BD=H，连PHBDACABCDPHBDPHACPH菱形面DBEPAEPABEBPABDPACBD面于作过面用心爱心专心PEDBFBFPAFDEBFB面于作过BF为所求PA=6，AH3，PH3，PB=2∴BE=DE=210，BD=2∴BF=15152另hSVVPADABDPABCDP31215152h（2）dPABCd,（BC，面PAD）=d（B，面PAD）=5152（3）过H作HM⊥PD于MHMPDHMMHACPDHAC面为公垂线231,2,3HMDHPDPH[例6]直二面角l，AB∩A，BAB，AB与所成角为，AB与所成角为，求证：2。用心爱心专心证明：过A作AC⊥l于C，过B作BD⊥l于D∴AC⊥BD⊥∠BAD=∠ABC=∴ABBDsin∴2ABBCBACsinBCBD∴BAC2BAC当且仅当C、D重合时，2[例7]如图所示，已知直线AB⊥平面，线段BC，CD⊥BC且CD与平面成30°的角，设AB=BC=CD=2，CE是CD在平面内的射影。（1）求证：AD与BC是异面直线；（2）求AC与DE之间距离；（3）求AD与BC所成角的度数。解析：（1）证明：假设AD与BC在同一个平面内， AB⊥，BC∴AB⊥BC，又CD⊥BC，∴AB//CD，∴CD⊥，这与CD与成30°角矛盾∴AD与BC是异面直线（2） CE是CD在平面内的射影∴DE⊥，从而DE⊥CE由BC⊥CD得BC⊥CE，由AB⊥，CE得CE⊥AB∴CE⊥平面ABC，AC平面ABC∴CE⊥AC∴CE是AC与DE的公垂线，CD=2，∠DCE=30°∴CE=3用心爱心专心（3）延长DE到F，使EF=DE，则DF//AB连接BF，则BF//AD∴∠FBC是AD与BC所成的角∴∠FBC=45°[例8]如图所示，四面体ABCS中，SA、SB、SC两两垂直，∠SBA=45°，∠SBC=60°，M为AB的中点，求：（1）BC与平面SAB所成的角；（2）SC与平面ABC所成角的正切值。解...