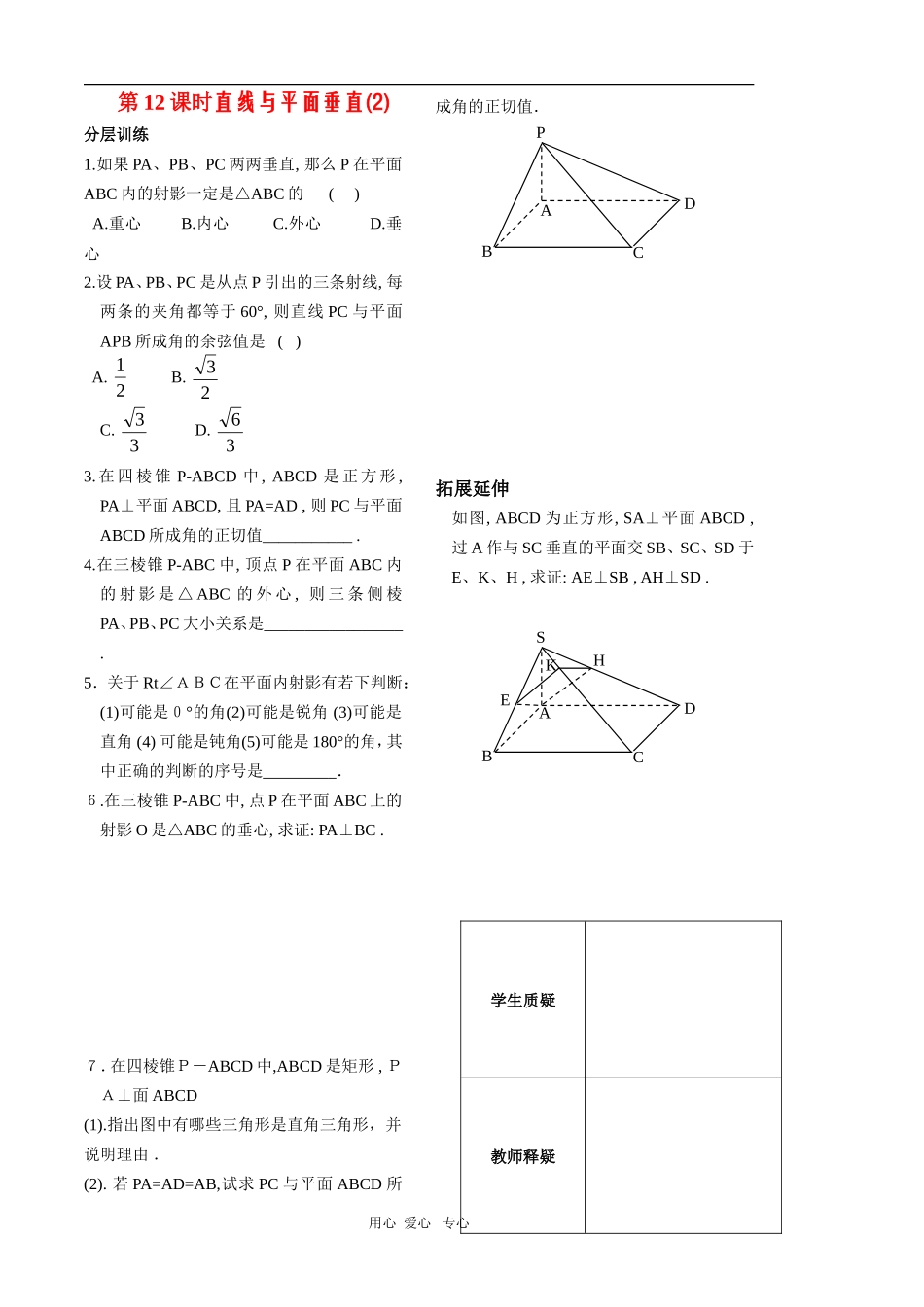
第12课时直线与平面垂直(2)分层训练1.如果PA、PB、PC两两垂直,那么P在平面ABC内的射影一定是△ABC的()A.重心B.内心C.外心D.垂心2.设PA、PB、PC是从点P引出的三条射线,每两条的夹角都等于60°,则直线PC与平面APB所成角的余弦值是()A.21B.23C.33D.363.在四棱锥P-ABCD中,ABCD是正方形,PA⊥平面ABCD,且PA=AD,则PC与平面ABCD所成角的正切值___________.4.在三棱锥P-ABC中,顶点P在平面ABC内的射影是△ABC的外心,则三条侧棱PA、PB、PC大小关系是_________________.5.关于Rt∠ABC在平面内射影有若下判断:(1)可能是0°的角(2)可能是锐角(3)可能是直角(4)可能是钝角(5)可能是180°的角,其中正确的判断的序号是.6.在三棱锥P-ABC中,点P在平面ABC上的射影O是△ABC的垂心,求证:PA⊥BC.7.在四棱锥P-ABCD中,ABCD是矩形,PA⊥面ABCD(1).指出图中有哪些三角形是直角三角形,并说明理由.(2).若PA=AD=AB,试求PC与平面ABCD所成角的正切值.拓展延伸如图,ABCD为正方形,SA⊥平面ABCD,过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:AE⊥SB,AH⊥SD.用心爱心专心学生质疑教师释疑ABCDHKESABCDP