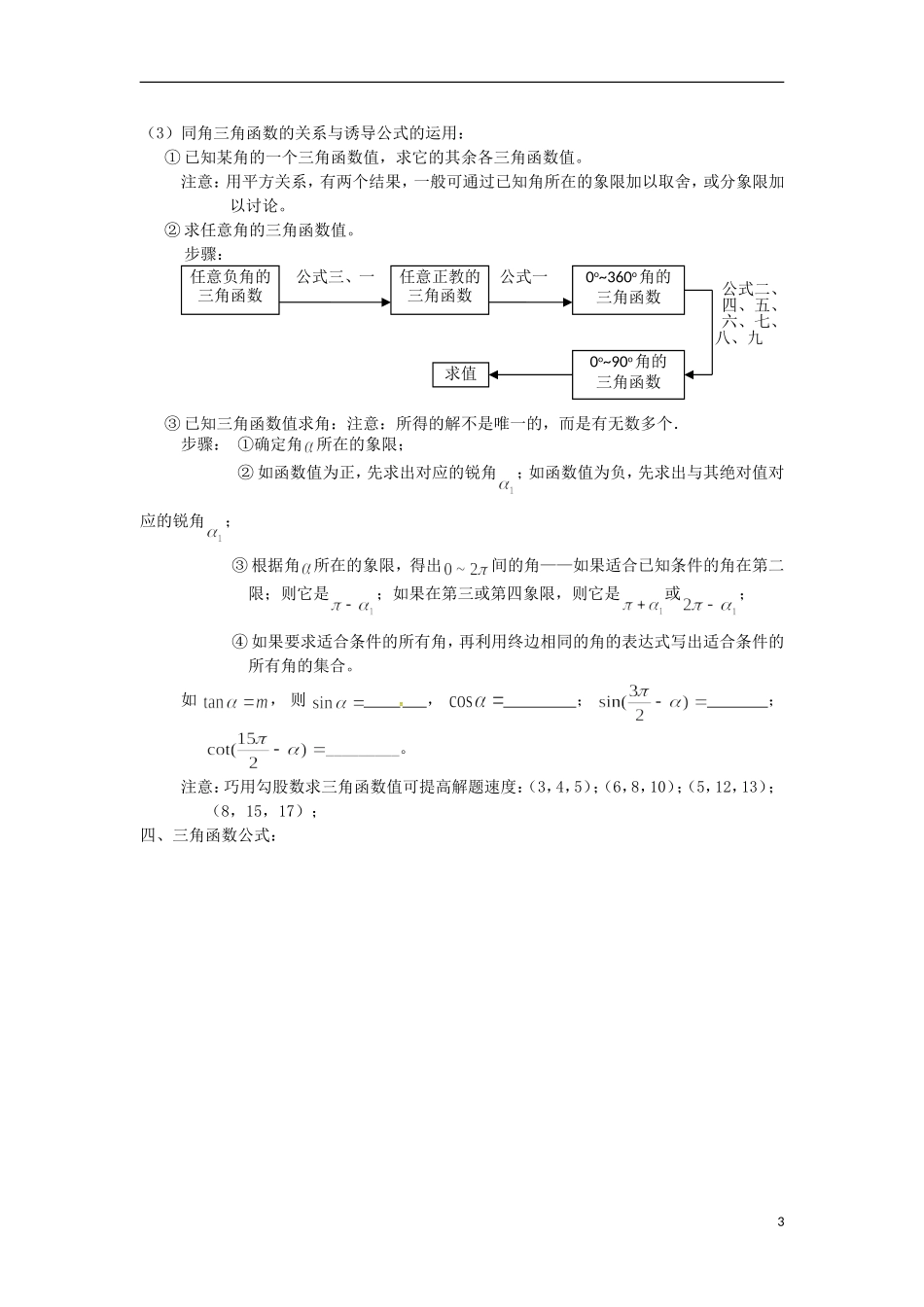
2015高三数学知识点汇总四、三角函数:一、角的概念和弧度制:(1)在直角坐标系内讨论角:角的顶点在原点,始边在轴的正半轴上,角的终边在第几象限,就说过角是第几象限的角。若角的终边在坐标轴上,就说这个角不属于任何象限,它叫象限界角。(2)①与角终边相同的角的集合:与角终边在同一条直线上的角的集合:;与角终边关于轴对称的角的集合:;与角终边关于轴对称的角的集合:;与角终边关于轴对称的角的集合:;②一些特殊角集合的表示:终边在坐标轴上角的集合:;终边在一、三象限的平分线上角的集合:;终边在二、四象限的平分线上角的集合:;终边在四个象限的平分线上角的集合:;(3)区间角的表示:①象限角:第一象限角:;第三象限角:;第一、三象限角:;②写出图中所表示的区间角:③④⑤⑥(4)正确理解角:要正确理解“间的角”=;“第一象限的角”=;“锐角”=;“小于的角”=;(5)由的终边所在的象限,通过来判断所在的象限。(6)弧度制:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零;任一已知角的弧度数的绝对值,其中为以角作为圆心角时所对圆弧的长,为圆的半径。(7)弧长公式:;半径公式:;扇形面积公式:;二、任意角的三角函数:(1)任意角的三角函数定义:以角的顶点为坐标原点,始边为轴正半轴建立直角坐标系,在角的终边上任取一个异于原点的点,点到原点的距离记为,则;;;;;;如:角的终边上一点,则。1xyOxyO(2)在图中画出角的正弦线、余弦线、正切线;比较,,,的大小关系:。(3)特殊角的三角函数值:0sincos三、同角三角函数的关系与诱导公式:(1)同角三角函数的关系平方关系是,,;倒数关系是,,;商式关系是,。作用:已知某角的一个三角函数值,求它的其余各三角函数值。(2)诱导公式::,,;:,,;:,,;:,,;:,,;:,,;:,,;:,,;:,,;诱导公式可用概括为:,。作用:求任意角的三角函数值。xyOaxyOaxyOayOa2(3)同角三角函数的关系与诱导公式的运用:①已知某角的一个三角函数值,求它的其余各三角函数值。注意:用平方关系,有两个结果,一般可通过已知角所在的象限加以取舍,或分象限加以讨论。②求任意角的三角函数值。步骤:③已知三角函数值求角:注意:所得的解不是唯一的,而是有无数多个.步骤:①确定角所在的象限;②如函数值为正,先求出对应的锐角;如函数值为负,先求出与其绝对值对应的锐角;③根据角所在的象限,得出间的角——如果适合已知条件的角在第二限;则它是;如果在第三或第四象限,则它是或;④如果要求适合条件的所有角,再利用终边相同的角的表达式写出适合条件的所有角的集合。如,则,;;_________。注意:巧用勾股数求三角函数值可提高解题速度:(3,4,5);(6,8,10);(5,12,13);(8,15,17);四、三角函数公式:任意负角的三角函数任意正教的三角函数0o~360o角的三角函数求值公式三、一公式一0o~90o角的三角函数公式二、四、五、六、七、八、九3三倍角公式:;;五、三角恒等变换:三角变换是运算化简的过程中运用较多的变换,提高三角变换能力,要学会创设条件,灵活运用三角公式,掌握运算,化简的方法和技能.常用的数学思想方法技__________________)cos(_____________________)](2cos[)sin(相除_________________)tan(_________________)sin(________________)cos(以代积化和差:以代以代和差化积倍角公式万能公式:________________2cos________________2sin22反解,以代半角公式:开方4巧如下:(1)角的变换:在三角化简,求值,证明中,表达式中往往出现较多的相异角,可根据角与角之间的和差,倍半,互补,互余的关系,运用角的变换,沟通条件与结论中角的差异,使问题获解,对角的变形如:①是的二倍;是的二倍;是的二倍;是的二倍;是的二倍;是的二倍;是的二倍。②;问:;;③;④;⑤;等等(2)函数名称变换:三角变形中,常常需要变函数名称为同名函数。如在三角函数中正余弦是基础,通常化切、割为弦,变异名为同名。(3)常数...