高三数学文第一轮复 习：立体几何基本概念和常见工具题人教版VIP免费

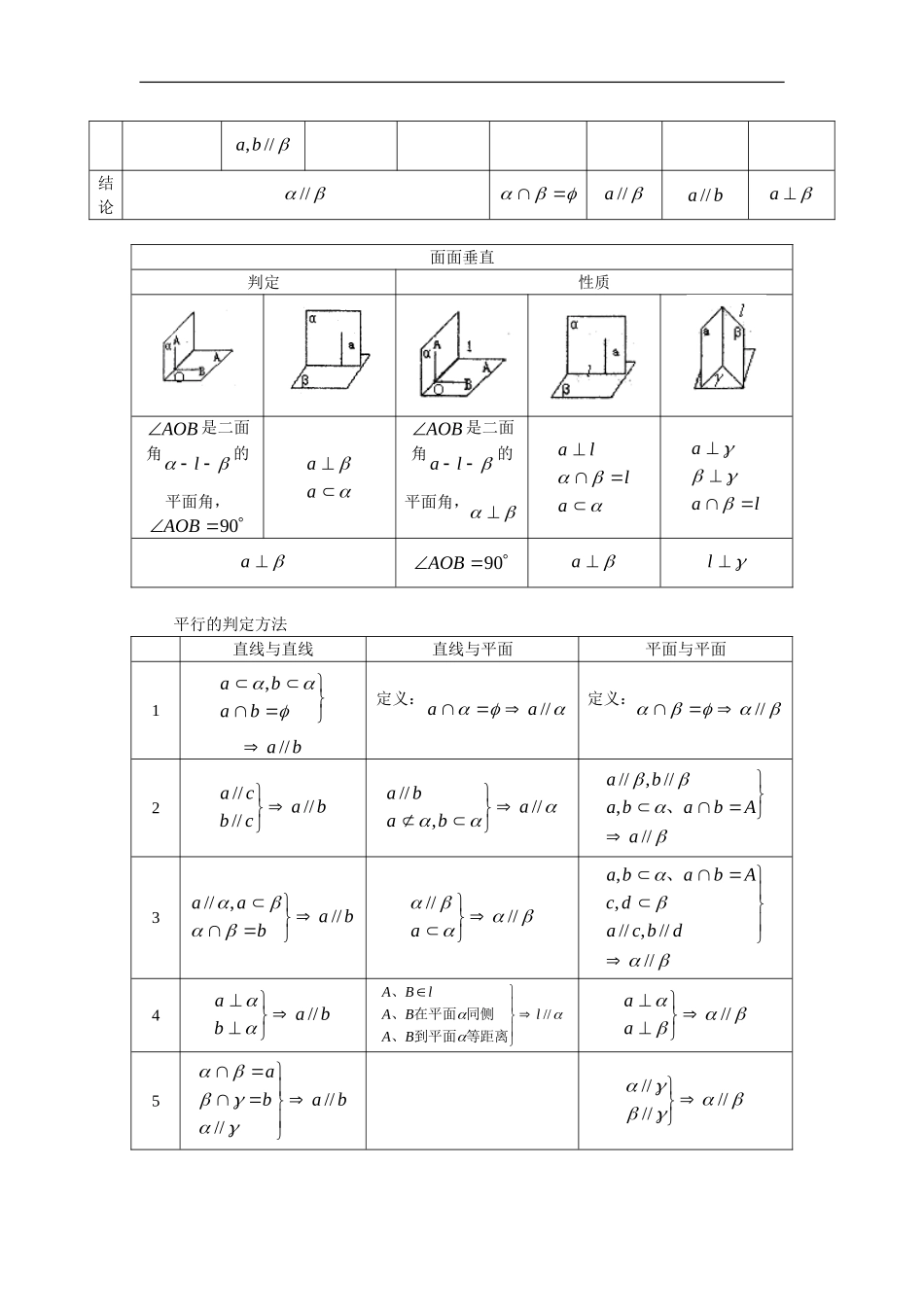
高三数学文第一轮复习：立体几何基本概念和常见工具题人教版【本讲教育信息】一.教学内容：立体几何基本概念和常见工具题类别线面平行判定性质图形条件ababa////abaa//结论//aaba//类别线面垂直判定性质图形条件bab是内任一直线cbacbcaba、、相交bba//baba结论ababa//类别面面平行判定性质图形条件ba,ba,相交aa//////a//ba//a////,ba结论////aba//a面面垂直判定性质AOB是二面角l的平面角，90AOBaaAOB是二面角la的平面角，allalaaa90AOBal平行的判定方法直线与直线直线与平面平面与平面1baba,ba//定义：//aa定义：//2bacbca////////,//ababa//,//,//aAbababa、3babaa//,//////a////,//,,dbcadcAbaba、4baba////lBABAlBA等距离到平面、同侧在平面、、//aa5baba//////////垂直的判定方法直线与直线直线与平面平面与平面1定义：90,0ObababaOObabbaa90,//,//定义：ababb)(任意定义：a与成90的二面角2baabal//aAcbcbcaba,,,aa3babaabba////4三垂线定理：babaabb,内的射影在为aa//5babaabb,内的射影在为alaal,,6aa,注：注重三种语言的学习：文字语言、图形语言、符号语言——三者是一个统一的整体。几个实用的工具题一.（1）证明几点共线的模型lPPP（2）找射影的一个模型已知：，l，a，则：l是a在内的射影（3）找点到平面内的射影若，l，A，则A到的距离等于A到l的距离（AO）（4）求点到平面的距离——转化的思想已知：A过A（找）直线//l，则l上任意一点到的距离二.若两异面直线垂直，找公垂线段的模型。“OK”其中一条异面直线作（找）一个平面与另一条异面直线垂直（存在且唯一），如图“OK”为公垂线段。三.空间四边形ABCD，若AB=AD，CB=CD（或：同底BD等腰的两个三角形构成的空间图形）方法：取BD中点P，连结AP，CP结论：（1）BD⊥平面APC（2）面APC⊥在ABD；面APC⊥面BCD（3）BD⊥AC（对棱）（4）∠APC是二面角A—BD—C的平面角（5）∠ACP是直线AC与面BCD所成的角∠CAP是直线AC与面ADB所成的角（6）在面APC内过P作PQ⊥AC于Q，则PQ是AC与BD的公垂线段。（7）由（2）知：过A作AA面BCD，垂足为A，则A一定在PC或PC延长线上。同理，过C作面ADB的垂线，垂足在哪儿？四.P为△ABC所在平面外一点，点P在平面ABC的射影为O。（1）若PA=PB=PC，则O为△ABC的外心（2）若P到三边AB、BC、CA的距离相等，则O是△ABC的内心或旁心。（3）若PA、PB、PC两两垂直，则O是△ABC的垂心。（4）若△ABC为正三角形，具备（1）、（2）、（3）条件之一时，则O是△ABC的中心。（5）若△ABC是Rt△，且PA=PB=PC，则O是△ABC斜边中点。五.如图在平面内，AP是平面的一条斜线。（1）若∠APC=∠APB（2）若A到PB，PC边距离相等。（3）AP在的射影是∠BPC的平分线以上三条有一个成立，便可推出另两个结论。即三组Rt△：APBAPC，OPBOPC，AOBAOC若有一组全等，则另两组必全等。【典型例题】[例1]在空间四边形ABCD中，E、F分别为AB、CD的中点，若AD=BC，且AD与BC成60°角，则异面直线EF和BC所成角的大小为（）A.30°B...