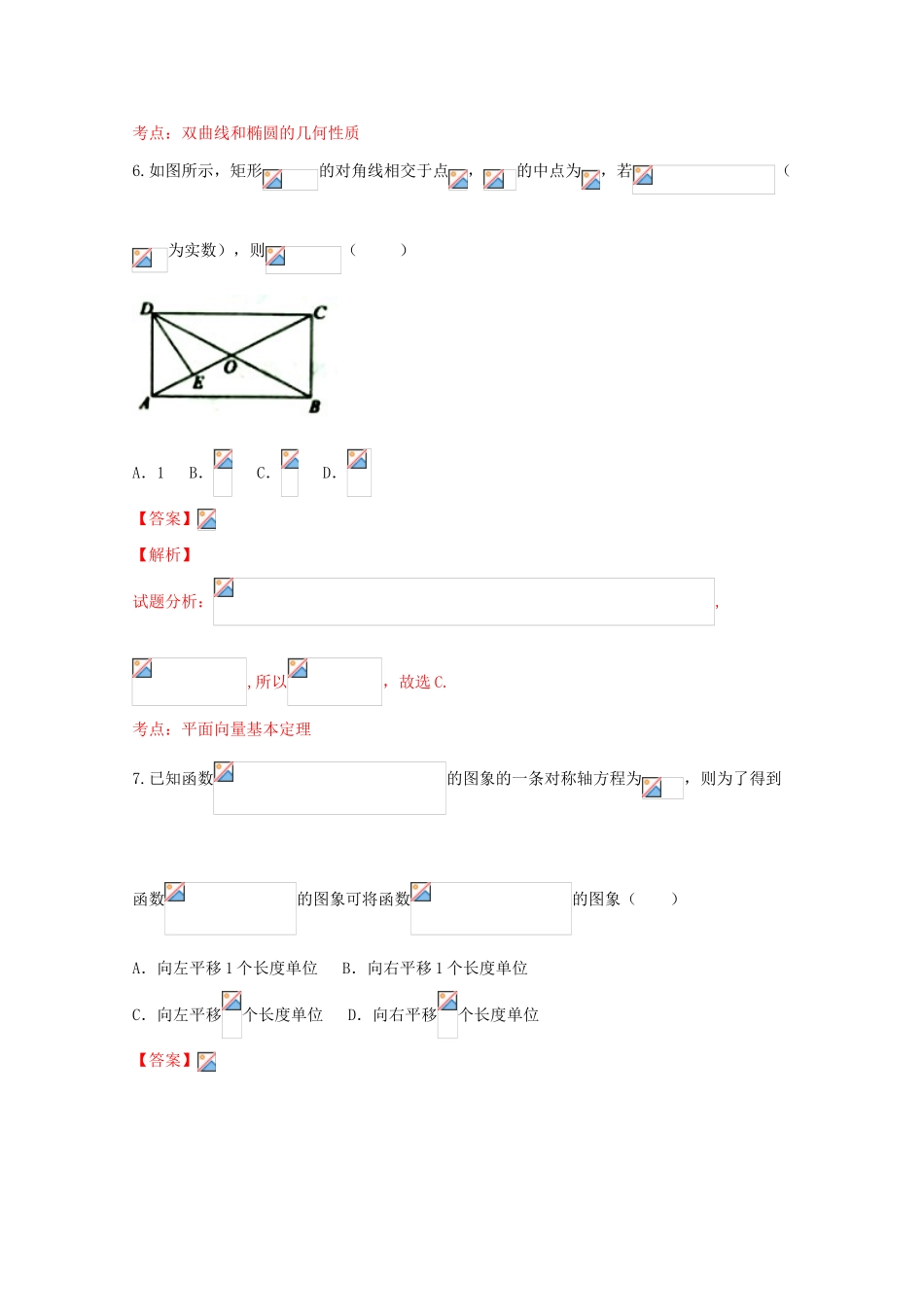
安徽省六安市第一中学2016届高三数学下学期第三次模拟考试试卷文(含解析)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,则()A.B.C.D.【答案】【解析】试题分析:,所以,故选C.考点:集合的运算2.若(为虚数单位),则直线的斜率为()A.-1B.1C.D.【答案】考点:1.复数;2.直线的斜率.3.已知正项等比数列中,其前项和为,若,则()A.B.C.D.【答案】【解析】试题分析:根据条件,解得,,,故选D.考点:等比数列4.若命题“,使不等式成立”为假命题,则实数的取值范围是()A.B.C.D.【答案】【解析】试题分析:原命题的否命题“,使不等式”为真命题,即,解得或,故选A.考点:特称命题的否定5.已知双曲线的顶点为椭圆的两个焦点,双曲线的右焦点与椭圆短轴的两个顶点构成正三角形,则双曲线的离心率为()A.B.C.D.2【答案】考点:双曲线和椭圆的几何性质6.如图所示,矩形的对角线相交于点,的中点为,若(为实数),则()A.1B.C.D.【答案】【解析】试题分析:,,所以,故选C.考点:平面向量基本定理7.已知函数的图象的一条对称轴方程为,则为了得到函数的图象可将函数的图象()A.向左平移1个长度单位B.向右平移1个长度单位C.向左平移个长度单位D.向右平移个长度单位【答案】考点:1.三角函数的性质;2.三角函数的图像变换.8.执行如图所示的程序框图,则输出的结果是()A.4B.5C.6D.7【答案】考点:循环结构9.如图1,已知正方体的棱长为,动点分别在线段上运动,当三棱锥的俯视图如图2时,三棱锥的左视图面积为()A.B.C.D.【答案】【解析】试题分析:根据俯视图可得点是的中点,点与重合,点在的中点,那么这四点所构成的几何体的左视图如图阴影表示,为正方形面积的一半,所以左视图的面积,故选C.考点:三视图10.设函数是定义在上的奇函数,且,则()A.-1B.-2C.1D.2【答案】考点:1.奇函数;2.分段函数求值.【一题多解】本题主要考察了奇函数的性质,属于基础题型,除了象本题根据奇函数的性质,求函数,也可以根据奇函数的性质不求函数,而直接求值,,那么,这样直接根据奇函数的性质求值,就比较快速,准确.11.已知成等差数列,且,则的取值范围是()A.B.C.D.【答案】【解析】试题分析:,即,,所以,解得,故选A.考点:1.等差数列的性质;2.基本不等式.【方法点睛】本题主要考察了基本不等式,属于基础题型,根据条件求的取值范围,所以涉及消掉另外两个量,所以根据条件,这样就消掉另外两个量了,常用的基本不等式和重要不等式包括,,.12.已知实数满足关系:,记满足上述关系的的集合为,则函数的最小值为()A.B.C.D.【答案】考点:1.导数的应用;2.基本不等式的应用.【方法点睛】本题主要考察了导数与基本不等式的综合应用,属于中档题型,第一个要解决的是函数的定义域,所以根据基本不等式,得到函数的定义域,根据导数求函数的最值,涉及了二次求导的问题,一次求导后,不易得到函数的单调性,所以需要二次求导,得到一次导的最小值,再判断函数的单调性,最后求最值.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知函数,若不等式的解集为,则的值为___________.【答案】考点:一元二次方程与韦达定理14.若实数满足,则的取值范围是__________.【答案】【解析】试题分析:如图,画出可行域,设写成表示斜率为-2的一组平行线,当直线过时,目标函数取得最小值,当直线过点时目标函数取得最大值,所以的取值范围是,故填:.考点:线性规划15.如图所示,椭圆的左,右顶点分别为,线段是垂直于椭圆长轴的弦,连接相交于点,则点的轨迹方程为____________.【答案】故填:.考点:1.轨迹方程;2.椭圆方程.【方法点睛】本题考查了交轨法求轨迹方程,属于中档题型,首先根据和两点的坐标,表示直线和,然后两个方程消参后就是交点的轨迹方程,消参多选择的方法多采用代入消参,或四则消参,比如两个式子相加,相减,或相除,相乘,再根据点在抛物线上,得到轨迹方程.16.数列满足,数列的前项和记为...