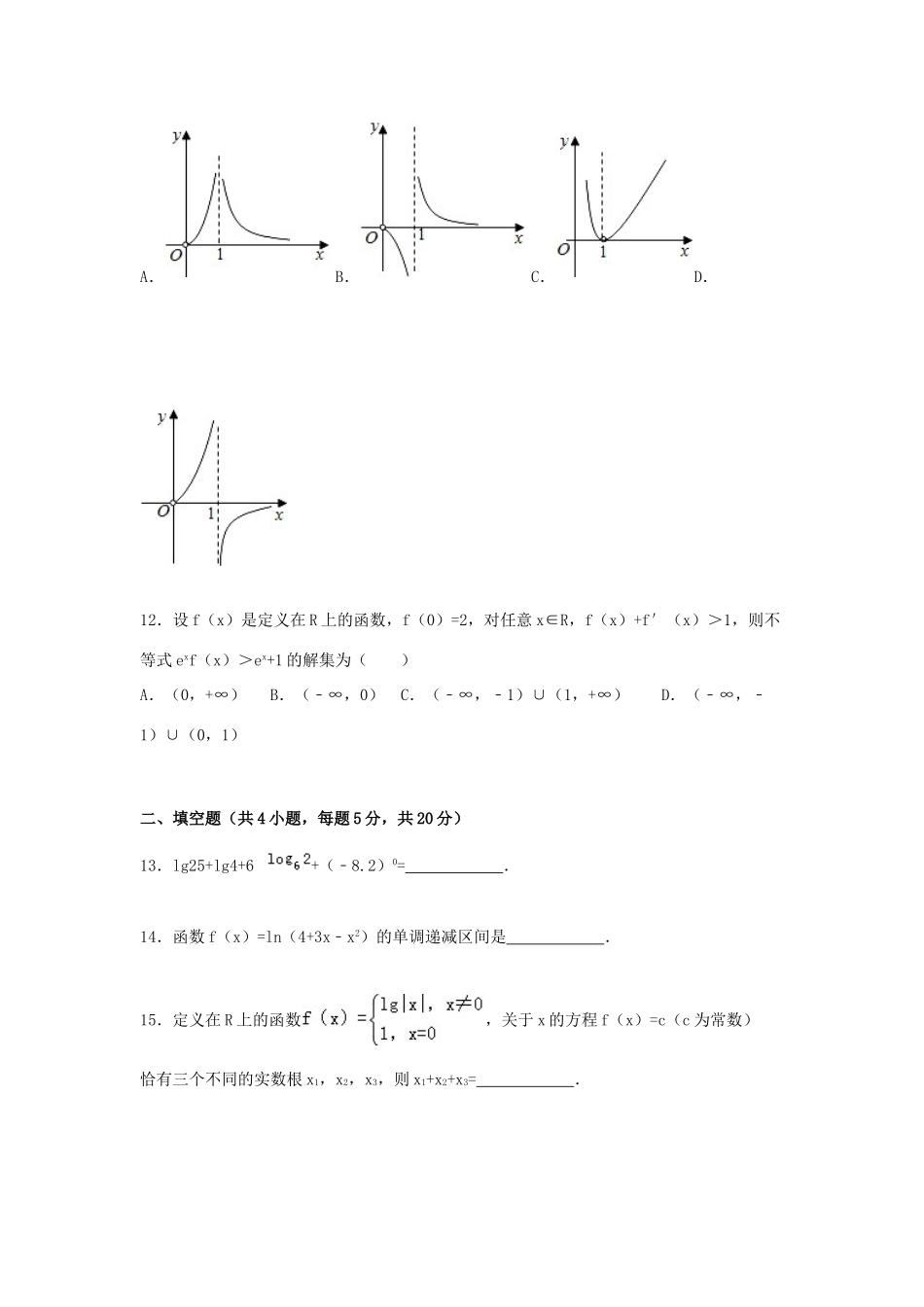
2015-2016学年四川省眉山中学高三(上)9月月考数学试卷(文科)一、选择题(共12小题,每小题5分,共60分)1.已知函数f(x)为偶函数,且当x<0时,f(x)=x﹣,那么f(1)=()A.0B.﹣2C.2D.12.已知命题p:∀x∈R,3x>0,则()A.¬p:∃x∈R,3x≤0B.¬p:∀x∈R,3x≤0C.¬p:∃x∈R,3x<0D.¬p:∀x∈R,3x<03.已知f(x)的定义域为[﹣1,3],则g(x)=的定义域为()A.[﹣2,6]B.[﹣2,1)∪(1,6]C.[﹣,]D.[﹣,1)∪(1,]4.对某杂志社一个月内每天收到的稿件数量进行了统计,得到样本的茎叶图(如图),则该样本的中位数、众数分别为()A.47、45B.45、47C.46、45D.45、465.设常数a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,则a的取值范围为()A.(﹣∞,2)B.(﹣∞,2]C.(2,+∞)D.[2,+∞)6.下列有关命题的叙述,①若p∨q为真命题,则p∧q为真命题;②“m>”是+=1为椭圆的充分必要条件;③“若x+y=0,则是x,y互为相反数”的逆命题为真命题;④命题“若x2﹣3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2﹣3x=2≠0”.其中错误的个数为()A.1B.2C.3D.47.曲线在点(1,﹣1)处的切线方程为()A.y=﹣2x+3B.y=﹣2x﹣3C.y=﹣2x+1D.y=2x+18.已知函数f(x)=﹣x3+2ax在(0,1]上是单调递增函数,则实数a的取值范围是()A.(﹣∞,)B.[,+∞)C.(,+∞)D.(﹣,)9.已知函数f(x)=ln(﹣3x)+1,则f(lg2)+f(lg)=()A.﹣1B.0C.1D.210.已知R上可导函数f(x)的图象如图所示,则不等式(x2﹣2x﹣3)f′(x)>0的解集为()A.(﹣∞,﹣2)∪(1,+∞)B.(﹣∞,﹣2)∪(1,2)C.(﹣∞,﹣1)∪(﹣1,0)∪(2,+∞)D.(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞)11.已知函数,则y=f(x)的图象大致为()A.B.C.D.12.设f(x)是定义在R上的函数,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式exf(x)>ex+1的解集为()A.(0,+∞)B.(﹣∞,0)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)二、填空题(共4小题,每题5分,共20分)13.lg25+lg4+6+(﹣8.2)0=.14.函数f(x)=ln(4+3x﹣x2)的单调递减区间是.15.定义在R上的函数,关于x的方程f(x)=c(c为常数)恰有三个不同的实数根x1,x2,x3,则x1+x2+x3=.16.若函数f(x)满足:在定义域D内存在实数x0,使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)为“1的饱和函数”.有下列函数:;③f(x)=lg(x2+2);④f(x)=cosπx,其中你认为是“1的饱和函数”的所有函数的序号为.三、解答题(共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.已知奇函数f(x)在定义域(﹣2,2)内是单调递增函数,求满足f(1﹣m)+f(1﹣3m)<0的实数m的取值范围.18.设有两个命题:命题p:函数f(x)=﹣x2+ax+1在[1,+∞)上是单调减函数;命题q:已知函数f(x)=2x3﹣6x2在[a,a+1]上单调递减,若命题p∨q为真,p∧q为假,求实数a的取值范围.19.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=﹣48x+8000,已知此生产线年产量最大为210吨.(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?20.已知函数f(x)=﹣x2+ax﹣lnx(a∈R).(1)当a=3时,求函数f(x)在上的最大值;(2)当函数f(x)在单调时,求a的取值范围.21.已知f(x)=ax2(a∈R),g(x)=2lnx.(1)讨论函数F(x)=f(x)﹣g(x)的单调性;(2)若方程f(x)=g(x)在区间[,e]上有两个不等解,求a的取值范围.22.已知函数f(x)=(e为自然对数的底数).(1)求函数f(x)的单调区间;(2)设函数φ(x)=xf(x)+tf′(x)+,存在函数x1,x2∈[0,1],使得成立2φ(x1)<φ(x2)成立,求实数t的取值范围.2015-2016学年四川省眉山中学高三(上)9月月考数学试卷(文科)参考答案与试题解...