高三数学一轮复习必备 第92-93课时 第十二章 极限——数列的极限、数学归纳法VIP免费

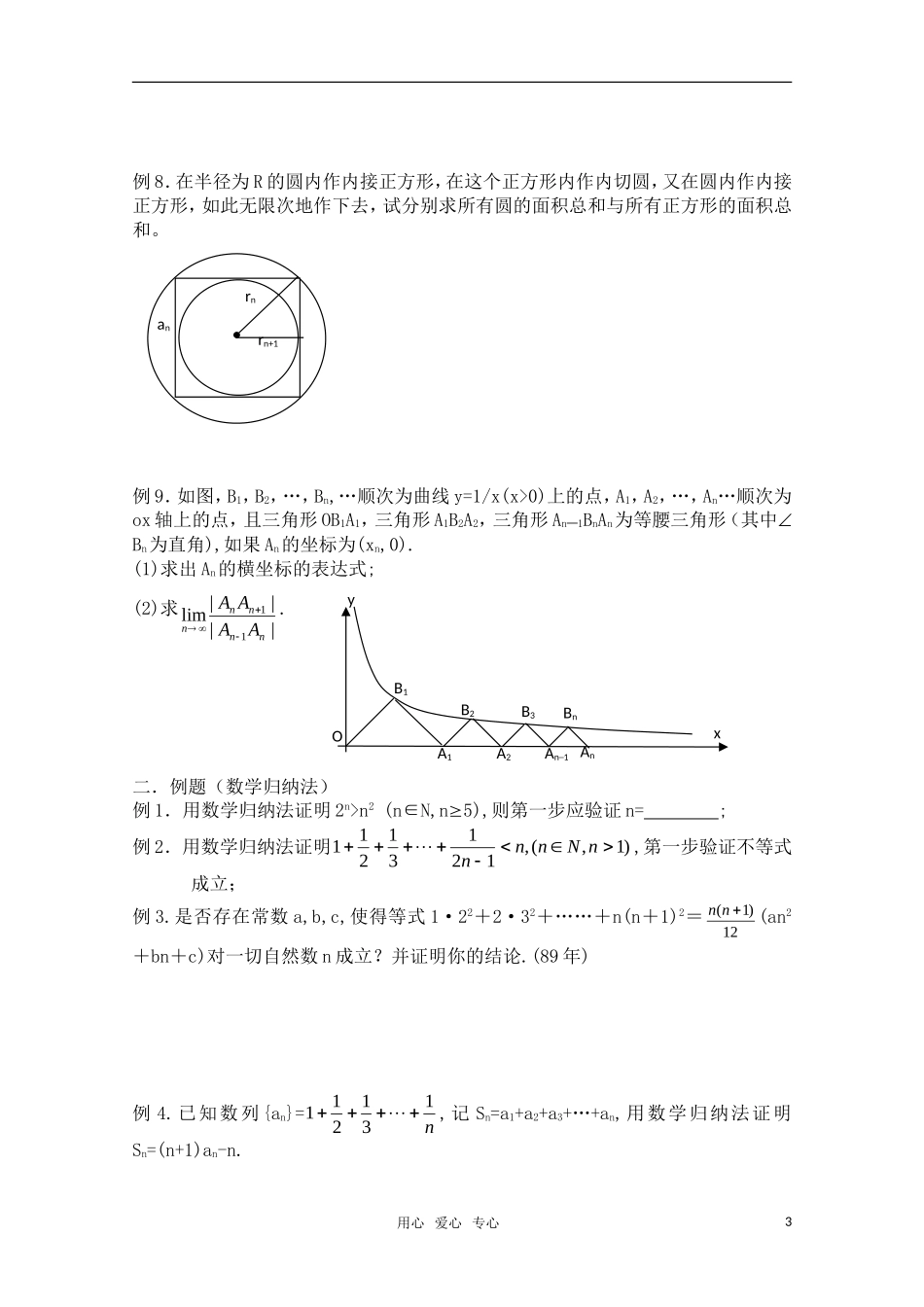
课题：数列的极限、数学归纳法一知识要点（一）数列的极限1.定义：对于无穷数列{an}，若存在一个常数A，无论预选指定多么小的正数，都能在数列中找到一项aN，使得当n>N时，|an-A|<恒成立，则称常数A为数列{an}的极限，记作Aannlim.2.运算法则：若limnna、limnnb存在，则有lim()limlimnnnnnnnabab；lim()limlimnnnnnnnabab)0lim(limlimlimnnnnnnnnnbbaba3.两种基本类型的极限：<1>S=)11()1(1)1(0limaaaaann或不存在<2>设()fn、()gn分别是关于n的一元多项式，次数分别是p、q，最高次项系数分别为pa、pb且)(0)(Nnng,则)()()(0)()(limqpqpbaqpngnfqpn不存在4.无穷递缩等比数列的所有项和公式：11aSq（|q|<1）无穷数列{an}的所有项和：limnnSS（当limnnS存在时）（二）数学归纳法数学归纳法是证明与自然数n有关命题的一种常用方法，其证题步骤为：①验证命题对于第一个自然数0nn成立。②假设命题对n=k(k≥0n)时成立,证明n=k+1时命题也成立.则由①②,对于一切n≥0n的自然数,命题都成立。二、例题（数学的极限）例1.（1）nlim112322nnn=;用心爱心专心12）．数列{an}和{bn}都是公差不为0的等差数列，且nnnbalim=3,则122limnnnaaanb=（3.）nlimnnaa211(a>1)=;（4）．2221321lim()111nnnnn=;（5）.)2(lim2nnnn=;（6）．等比数列{an}的公比为q=─1/3,则nnnaaaaaa24221lim=;例2．将无限循环小数21.0；1.3221化为分数.例3．已知1)11(lim2bannnn,求实数a,b的值;例4．数列{an},{bn}满足nlim(2an+bn)=1,nlim(an─2bn)=1,试判断数列{an},{bn}的极限是否存在，说明理由并求nlim(anbn)的值.例5．设首项为a，公差为d的等差数列前n项的和为An,又首项为a,公比为r的等比数列前n项和为Gn,其中a≠0,|r|<1.令Sn=G1+G2+…+Gn,若有lim()nnnASn=a,求r的值.例6．设首项为1，公比为q(q>0)的等比数列的前n项之和为Sn,又设Tn=1(1,2,)nnSnS,求nnTlim.例7．{an}的相邻两项an,an+1是方程x2─cnx+n)31(=0的两根，又a1=2,求无穷等比c1,c2,…cn,…的各项和.用心爱心专心2例8．在半径为R的圆内作内接正方形，在这个正方形内作内切圆，又在圆内作内接正方形，如此无限次地作下去，试分别求所有圆的面积总和与所有正方形的面积总和。例9．如图，B1，B2，…，Bn,…顺次为曲线y=1/x(x>0)上的点，A1，A2，…，An…顺次为ox轴上的点，且三角形OB1A1，三角形A1B2A2，三角形An─1BnAn为等腰三角形（其中Bn为直角),如果An的坐标为(xn,0).(1)求出An的横坐标的表达式;(2)求||||lim11nnnnnAAAA.二．例题（数学归纳法）例1．用数学归纳法证明2n>n2(n∈N,n5),则第一步应验证n=;例2．用数学归纳法证明)1,(,12131211nNnnn,第一步验证不等式成立；例3.是否存在常数a,b,c,使得等式1·22＋2·32＋……＋n(n＋1)2＝12)1(nn(an2＋bn＋c)对一切自然数n成立？并证明你的结论.(89年)例4.已知数列{an}=n131211,记Sn=a1+a2+a3+…+an,用数学归纳法证明Sn=(n+1)an-n.用心爱心专心3An─1A1A2AnBnB3B2B1yxOrnrn+1an例5．证明：n2131211>22n(n∈N,n2)例6．证明：xn─nan─1x+(n─1)an能被(x─a)2整除(a≠0).例7.在1与2之间插入n个正数naaaa,,,,321，使这2n个数成等比数列；又在1与2之间插入n个正数nbbbb,,,,321使这2n个数成等差数列．记nnnnbbbbBaaaaA321321,．（Ⅰ）求数列nA和nB的通项；（Ⅱ）当7n时，比较nA与nB的大小，并证明你的结论．例8．若数列{an}满足对任意的n有：Sn=2)(1naan,试问该数列是怎样的数列？并证明你的结论.例9．已知数列bn是等差数列，bbbb112101145，…。（Ⅰ）求数列bn的通项bn；（Ⅱ）设数列na的通项abnanlog11（其中a0，且a1），记Sn是数列an的前n项和。试比较Sn与131loganb的大...