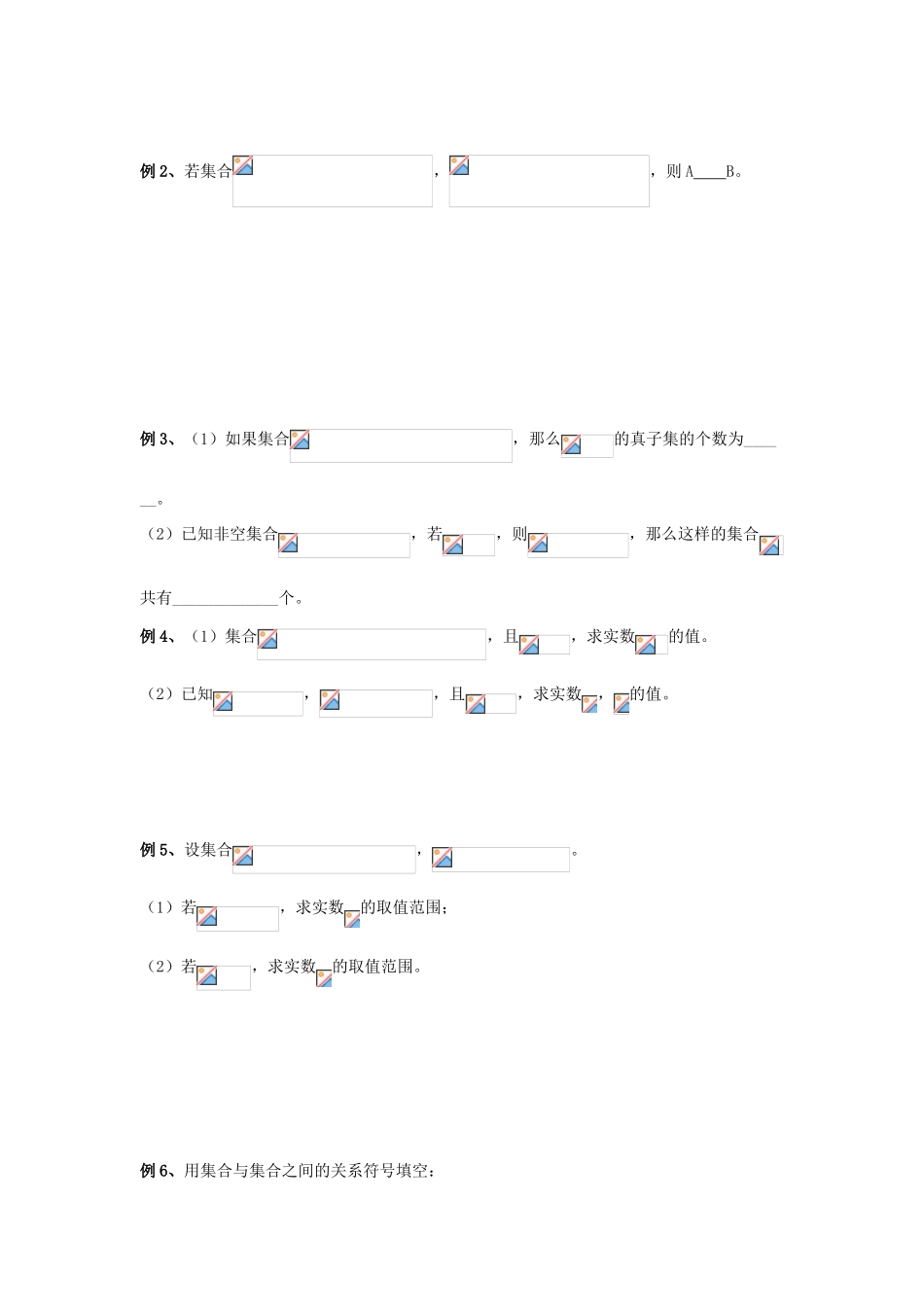
集合概念与应用一、知识导学:1.集合的概念:把某些能确切指定的对象的全体看作一个整体,这个整体形成一个集合,每个对象为该集合的元素。2.集合元素的特性:确定性:对于一个给定的集合,任何一个对象都能被确切地判断是否为该集合中的元素。互异性(唯一性):对于集合,内含条件。无序性:3.集合的表示方法:列举法:描述法:图示法:常见集合类型:数集,点集。4.集合与集合的关系:子集(个数):真子集:集合相等:空集的性质:空集是任何集合的子集,是任何非空集合的真子集。5.集合的运算交集:并集:补集:二、例题导讲:例1、将下列集合用列举法表示:(1)集合;(2)集合。例2、若集合,,则AB。例3、(1)如果集合,那么的真子集的个数为______。(2)已知非空集合,若,则,那么这样的集合共有_____________个。例4、(1)集合,且,求实数的值。(2)已知,,且,求实数,的值。例5、设集合,。(1)若,求实数的取值范围;(2)若,求实数的取值范围。例6、用集合与集合之间的关系符号填空:(1)(2)(3)(4)【集合及运算练习】一、填空题:1.设全集U=Z,A={1,3,5,7,9},B={1,2,3,4,5,6},则右图中阴影部分表示的集合是{}。2.已知集合,则__。3.满足的集合M共有个。4.集合是单元素集合,则实数。5.已知集合=,,则=。6.若集合A=,B=,且,则实数的取值范围是。7.已知集合,则=。8.集合___________。9.集合A={x||x|≤4,x∈R},B{x||x-3|≤a,x∈R},且A⊇B,则实数a的取值范围是。10.设表示不大于的最大整数,集合,,则___________。二、选择题:11.已知集合、,若不是的子集,则下列命题中正确的是()A.对任意的,都有;B.对任意的,都有;C.存在,满足,;D.存在,满足,.12.已知全集U=N*,集合A={x|x=2n,n∈N*},B={x|x=4n,n∈N},则()A.U=A∪BB.U=(A)∪BC.U=A∪(B)D.U=(A)∪(B)13.已知集合P={(x,y)||x|+|y|=1},Q={(x,y)|x2+y2≤1},则()A.PQB.P=QC.PQD.P∩Q=Q14.若x∈A则∈A,就称A是伙伴关系集合,集合M={-1,0,,,1,2,3,4}的所有非空子集中,具有伙伴关系的集合的个数为()A.15B.16C.28D.25三、解答题:15.设,若,求所有满足条件的实数的集合。16.已知全集,A={1,},如果,则这样的实数是否存在?若存在,求出,若不存在,说明理由。17.设集合,,求实数m的取值范围。18.已知集合,求实数b的取值范围。【命题和条件练习】一、填空题:1.设是方程的两实数根;,则是的_____________条件。2.是成立的_____________条件。3.已知命题:“”(1)该命题的一个充分非必要条件是___________;(2)该命题的一个必要非充分条件是___________。4.命题“面积不相等的两个三角形不全等”的逆否命题是。5.有4个命题:(1)没有男生爱踢足球;(2)所有男生都不爱踢足球;(3)至少有一个男生不爱踢足球;(4)所有女生都爱踢足球;其中是命题“所有男生都爱踢足球”的否定是_______。6.“”是“”成立的条件。7.“”的条件。8.已知若是的充分不必要条件,则实数的取值范围是________________。9.已知数列的通项公式为,则数列{}成等比数列是数列的通项公式为的条件。10.定义:若对定义域上的任意实数都有,则称函数为上的零函数.根据以上定义,“是上的零函数或是上的零函数”为“与的积函数是上的零函数”的条件。二、选择题:11.设m,n是整数,则“m,n均为偶数”是“m+n是偶数”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件12.若非空集合满足,且不是的子集,则()A.“”是“”的充分条件但不是必要条件B.“”是“”的必要条件但不是充分条件C.“”是“”的充要条件D.“”既不是“”的充分条件也不是“”必要条件13.命题“若不正确,则不正确”的逆命题的等价命题是()A.若不正确,则不正确B.若不正确,则正确C.若正确,则不正确D.若正确,则正确14.设全集为,有以下四个命题:(1)(2)(3)(4)其中是命题的充要条件的有______个。()A.1个B.2个C.3个D.4个15.给出下面类比推理命题(其中Q为有理数...