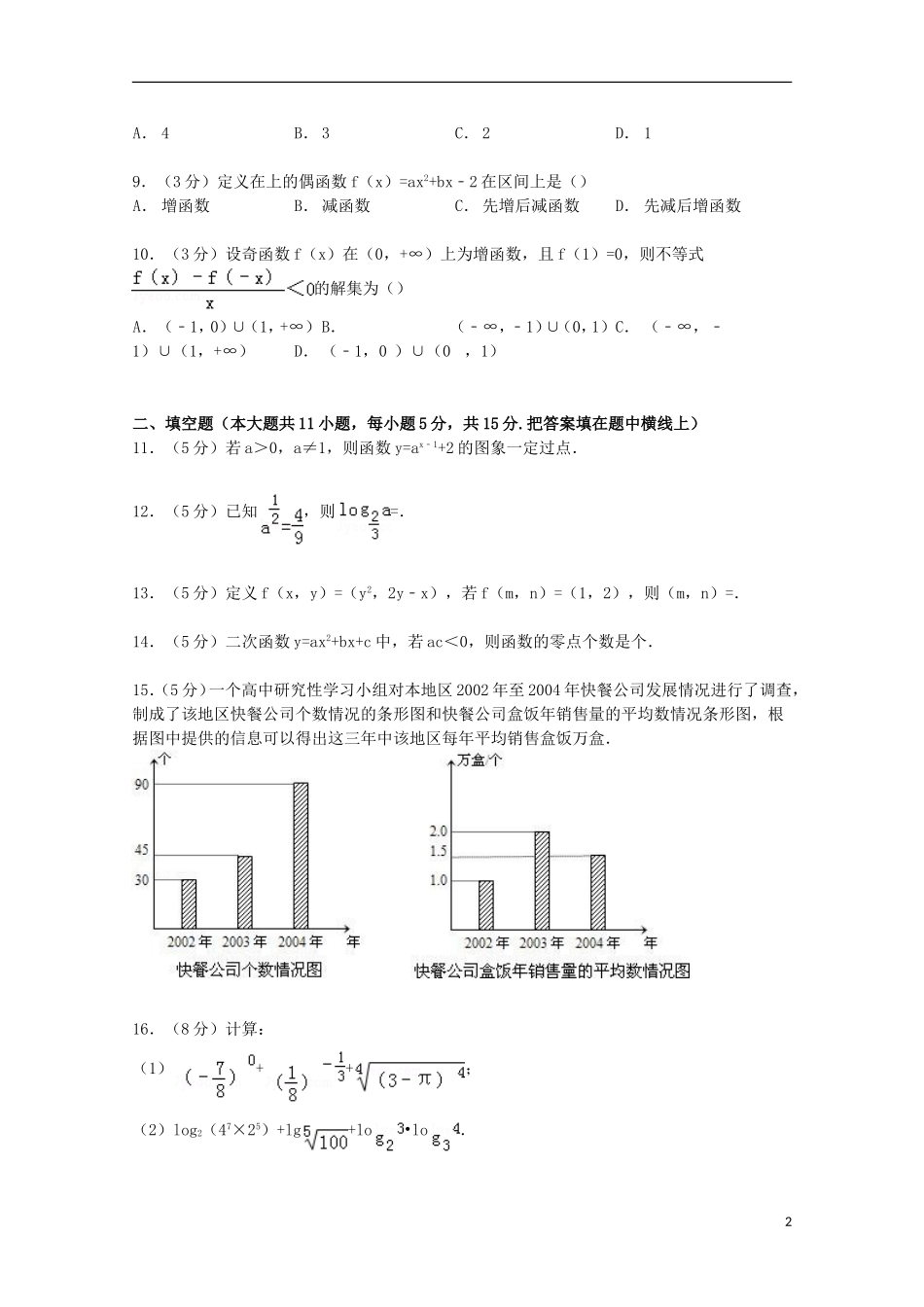
福建省莆田一中2014-2015学年高一上学期第一次段考数学试卷一、选择题(本大题共10小题,每小题3分,共30分.每小题只有一个正确答案)1.(3分)如图,可表示函数y=f(x)的图象的只能是()A.B.C.D.2.(3分)函数y=的定义域为()A.(0,e]B.(﹣∞,e]C.(0,10]D.(﹣∞,10]3.(3分)已知函数f(+1)=x+1,则函数f(x)的解析式为()A.f(x)=x2B.f(x)=x2+1(x≥1)C.f(x)=x2﹣2x+2(x≥1)D.f(x)=x2﹣2x(x≥1)4.(3分)已知全集U={1,2,3,4,5},集合A={x|x2﹣3x+2=0},B={x|x=2a,a∈A},则集合∁U(A∪B)中元素的个数为()A.1B.2C.3D.45.(3分)设a∈,则使函数y=xa的定义域是R,且为奇函数的所有a的值是()A.1,3B.﹣1,1C.﹣1,3D.﹣1,1,36.(3分)三个数60.7,0.76,log0.76的大小顺序是()A.0.76<60.7<log0.76B.0.76<log0.76<60.7C.log0.76<60.7<0.76D.log0.76<0.76<60.77.(3分)设f(x)=3x+3x﹣8,用二分法求方程3x+3x﹣8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间()A.(1,1.25)B.(1.25,1.5)C.(1.5,2)D.不能确定8.(3分)函数的图象和函数g(x)=log2x的图象的交点个数是()1A.4B.3C.2D.19.(3分)定义在上的偶函数f(x)=ax2+bx﹣2在区间上是()A.增函数B.减函数C.先增后减函数D.先减后增函数10.(3分)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式的解集为()A.(﹣1,0)∪(1,+∞)B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,0)∪(0,1)二、填空题(本大题共11小题,每小题5分,共15分.把答案填在题中横线上)11.(5分)若a>0,a≠1,则函数y=ax﹣1+2的图象一定过点.12.(5分)已知,则=.13.(5分)定义f(x,y)=(y2,2y﹣x),若f(m,n)=(1,2),则(m,n)=.14.(5分)二次函数y=ax2+bx+c中,若ac<0,则函数的零点个数是个.15.(5分)一个高中研究性学习小组对本地区2002年至2004年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图,根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭万盒.16.(8分)计算:(1)++;(2)log2(47×25)+lg+lo•lo.217.(8分)A={x|﹣2<x≤5},B={x|m+1≤x≤2m﹣1},若B⊆A,则m的取值范围是.18.(8分)已知函数f(x)=x2+(lga+2)x+lgb,﹣1是函数F(x)=f(x)+2的一个零点,且对于任意x∈R,恒有f(x)≥2x成立,求实数a,b的值.19.(8分)某工厂生厂了一种电子元件,每月生产的数据如表:月份1234产量(千件)505256.263.5为估计一年内每月该电子元件的产量,以这4个月的产量为依据,拟选用y=ax+b或y=ax+b为拟合函数,来模拟电子元件的产量y与月份x的关系.请问:哪个函数较好?并由此估计5月份的产量.20.(11分)已知函数f(x)=a﹣.(1)求证:不论a为何实数f(x)总是为增函数;(2)确定a的值,使(x)为奇函数;(3)当f(x)为奇函数时,求f(x的值域.21.(12分)已知:函数f(x)对一切实数x,y都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.(1)求f(0)的值.(2)求f(x)的解析式.(3)已知a∈R,设P:当0<x<时,不等式f(x)+3<2x+a恒成立;Q:当x∈时,g(x)=f(x)﹣ax是单调函数.如果满足P成立的a的集合记为A,满足Q成立的a的集合记为B,求A∩∁RB(R为全集).福建省莆田一中2014-2015学年高一上学期第一次段考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分.每小题只有一个正确答案)1.(3分)如图,可表示函数y=f(x)的图象的只能是()A.B.C.D.3考点:抽象函数及其应用.专题:函数的性质及应用.分析:本题利用函数的定义,对于定义域内的任意的自变量x,有唯一的函数值与之对应,判断出那个图形符合函数的对应法则,得到本题结论.解答:解:根据函数的定义,对于定义域内的任意的一个自变量x,有唯一的函数值与之对应,故任作一条垂直于x轴的直线,与函...