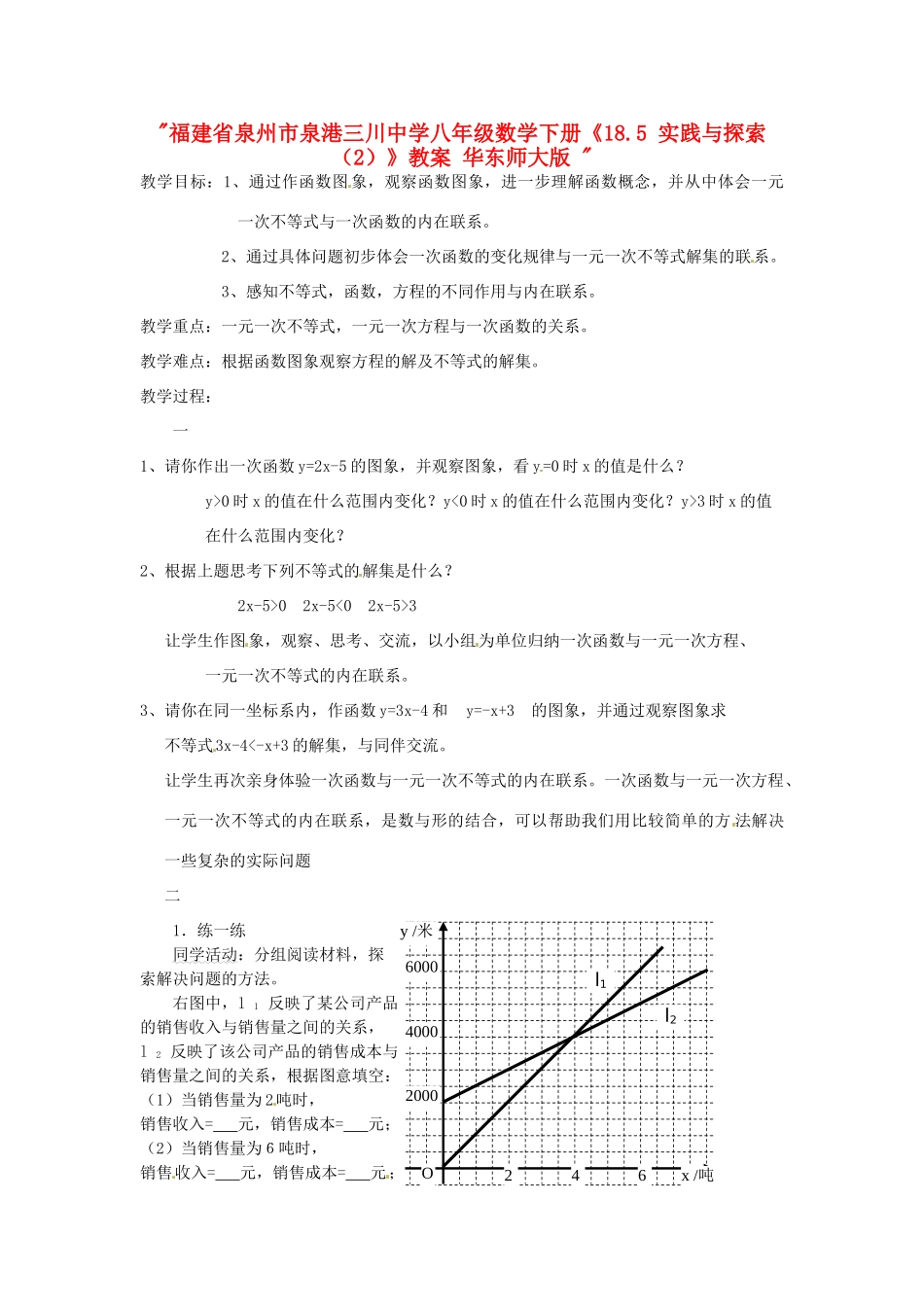
"福建省泉州市泉港三川中学八年级数学下册《18.5实践与探索(2)》教案华东师大版"教学目标:1、通过作函数图象,观察函数图象,进一步理解函数概念,并从中体会一元一次不等式与一次函数的内在联系。2、通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。3、感知不等式,函数,方程的不同作用与内在联系。教学重点:一元一次不等式,一元一次方程与一次函数的关系。教学难点:根据函数图象观察方程的解及不等式的解集。教学过程:一1、请你作出一次函数y=2x-5的图象,并观察图象,看y=0时x的值是什么?y>0时x的值在什么范围内变化?y<0时x的值在什么范围内变化?y>3时x的值在什么范围内变化?2、根据上题思考下列不等式的解集是什么?2x-5>02x-5<02x-5>3让学生作图象,观察、思考、交流,以小组为单位归纳一次函数与一元一次方程、一元一次不等式的内在联系。3、请你在同一坐标系内,作函数y=3x-4和y=-x+3的图象,并通过观察图象求不等式3x-4<-x+3的解集,与同伴交流。让学生再次亲身体验一次函数与一元一次不等式的内在联系。一次函数与一元一次方程、一元一次不等式的内在联系,是数与形的结合,可以帮助我们用比较简单的方法解决一些复杂的实际问题二1.练一练同学活动:分组阅读材料,探索解决问题的方法。右图中,l1反映了某公司产品的销售收入与销售量之间的关系,l2反映了该公司产品的销售成本与销售量之间的关系,根据图意填空:(1)当销售量为2吨时,销售收入=元,销售成本=元;(2)当销售量为6吨时,销售收入=元,销售成本=元;y/米6000l2240002000x/吨46Ol1(3)当销售量=吨时,销售收入等于销售成本;(4)当销售量吨时,该公司赢利(销售收入大于销售成本);当销售量吨时,该公司亏损(销售收入小于销售成本);(5)l1对应的函数表达式是,l2对应的函数表达式是。师生互动:利用课件共同讨论,并就此课题内容探讨你的发现。2.议一议师生共同活动:我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派快艇B追赶,下图中l1l2分别表示B船离岸起两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。根据图象回答下列问题:(1)哪条线表示B到海岸的距离与追赶时间之间的关系?(2)A、B哪个速度快?(3)15分钟内B能否追上A?(4)如果一直追下去,那么B能否追上A?(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?3.做一做新龟兔赛跑(问题探讨)这一次兔子全力以赴拿下了比赛。下图l1l2分别是龟兔赛跑中路程与时间之间的函数图象。根据图象可以知道:(1)这是一次米赛跑。(2)表示兔子的图象是。(3)这一次先到达终点的是。(4)当兔子到达终点时,乌龟距终点还有米。(5)乌龟要与兔子同时到达终点,乌龟要先跑米。(6)乌龟要先到达终点,至少要比兔子早跑分钟。l2l1S/海里42t/分812O64108三、小结与反思1、想一想你能用其他方法解决上述问题吗?2、当坐标系中,出现两个或多个函数图象时,可先分别获取每一个函数图象的信息,在此基础上再整合不同函数图象的信息,获得不同函数间的综合信息。四、作业X