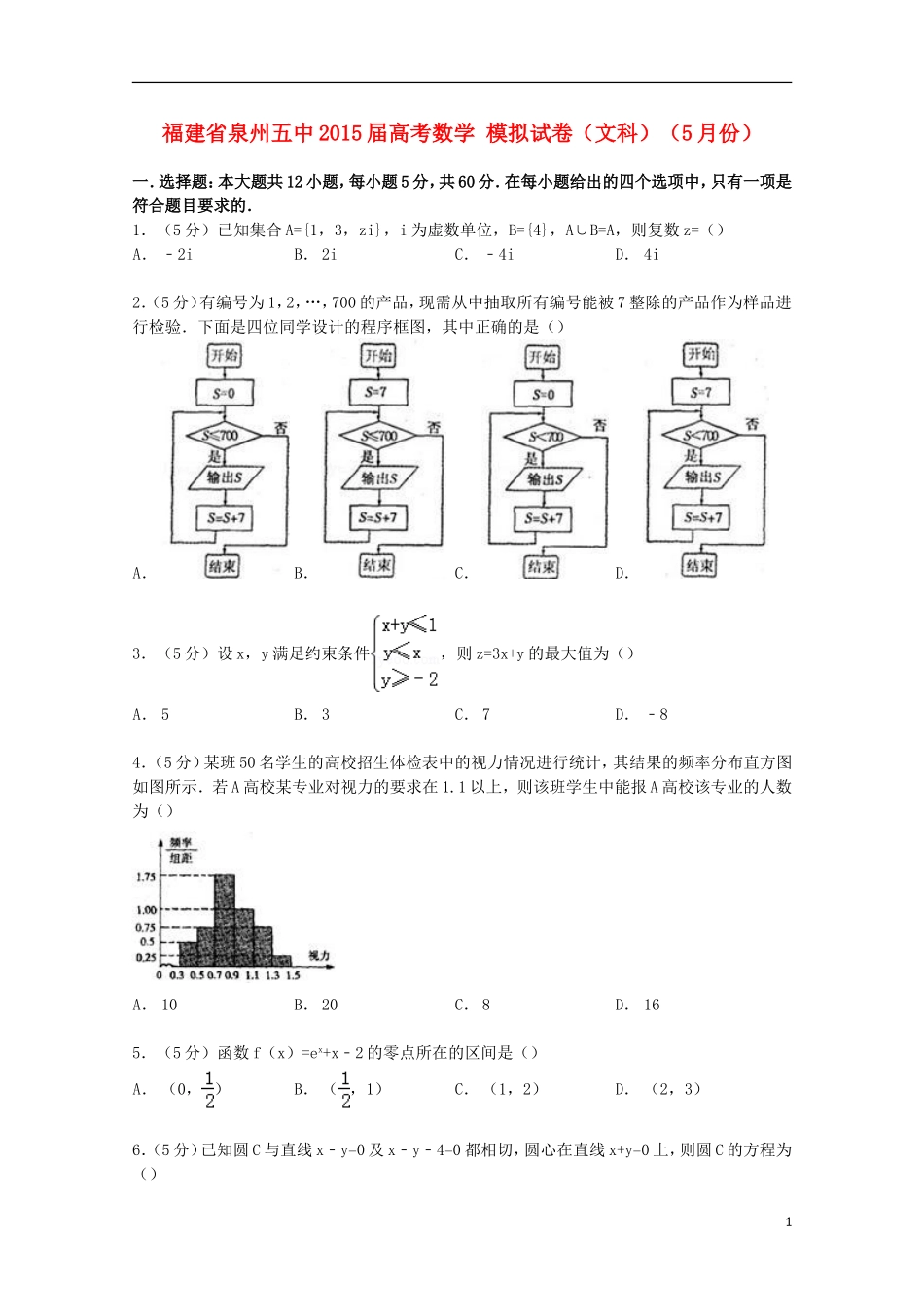
福建省泉州五中2015届高考数学模拟试卷(文科)(5月份)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={1,3,zi},i为虚数单位,B={4},A∪B=A,则复数z=()A.﹣2iB.2iC.﹣4iD.4i2.(5分)有编号为1,2,…,700的产品,现需从中抽取所有编号能被7整除的产品作为样品进行检验.下面是四位同学设计的程序框图,其中正确的是()A.B.C.D.3.(5分)设x,y满足约束条件,则z=3x+y的最大值为()A.5B.3C.7D.﹣84.(5分)某班50名学生的高校招生体检表中的视力情况进行统计,其结果的频率分布直方图如图所示.若A高校某专业对视力的要求在1.1以上,则该班学生中能报A高校该专业的人数为()A.10B.20C.8D.165.(5分)函数f(x)=ex+x﹣2的零点所在的区间是()A.(0,)B.(,1)C.(1,2)D.(2,3)6.(5分)已知圆C与直线x﹣y=0及x﹣y﹣4=0都相切,圆心在直线x+y=0上,则圆C的方程为()1A.(x+1)2+(y﹣1)2=2B.(x﹣1)2+(y+1)2=2C.(x﹣1)2+(y﹣1)2=2D.(x+1)2+(y+1)2=27.(5分)已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.(5分)若a>0,b>0,且a+2b﹣2=0,则ab的最大值为()A.B.1C.2D.49.(5分)设函数f(x)=x2﹣2x+m,m∈R.若在区间上随机取一个数x,f(x)<0的概率为,则m的值为()A.2B.﹣2C.3D.﹣310.(5分)已知△ABC中,内角A,B,C所对的边长分别为a,b,c.若a=2bcosA,B=,c=1,则△ABC的面积等于()A.B.C.D.11.(5分)过双曲线的左焦点F(﹣c,0)(c>0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P.若,则双曲线的离心率为()A.B.C.D.12.(5分)对于函数f(x),若存在区间A=,使得{y|y=f(x),x∈A}=A,则称函数f(x)为“可等域函数”,区间A为函数f(x)的一个“可等域区间”.给出下列4个函数:①f(x)=sin(x);②f(x)=2x2﹣1;③f(x)=|1﹣2x|;④f(x)=log2(2x﹣2).其中存在唯一“可等域区间”的“可等域函数”为()A.①②③B.②③C.①③D.②③④二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡相应位置.13.(4分)已知tanθ=2,则sin2θ﹣sinθcosθ+cos2θ=.214.(4分)设向量,,则向量在向量方向上的投影为.15.(4分)已知函数f(x)满足:x≥4,则f(x)=2x;当x<4时f(x)=f(x+1),则f(2+log3)=.16.(4分)点集{(x,y)|||x|﹣1|+|y|=2}的图形是一条封闭的折线,这条封闭折线所围成的区域的面积是.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(12分)从一批草莓中,随机抽取n个,其重量(单位:克)的频率分布表如下:分组(重量)19.(12分)设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b3=9,a5+b5=25.(Ⅰ)求{an},{bn}的通项公式;(Ⅱ)求数列的前n项和Sn.20.(12分)如图,梯形ABCD中,CE⊥AD于E,BF⊥AD于F,且AF=BF=BC=1,DE=,现将△ABF,△CDE分别沿BF与CE翻折,使点A与点D重合.(Ⅰ)设面ABF与面CDE相交于直线l,求证:l∥CE;(Ⅱ)试类比求解三角形的内切圆(与三角形各边都相切)半径的方法,求出四棱锥A﹣BCEF的内切球(与四棱锥各个面都相切)的半径.21.(12分)设P是圆x2+y2=a2(a>0)上的动点,点D是点P在x轴上的投影,M为PD上一点,且(a>b>0).(Ⅰ)求证:点M的轨迹Γ是椭圆;(Ⅱ)设(Ⅰ)中椭圆Γ的左焦点为F,过F点的直线l交椭圆于A,B两点,C为线段AB的中点,当三角形CFO(O为坐标原点)的面积最大时,求直线l的方程.322.(14分)已知函数,(Ⅰ)求函数f(x)的单调区间,并判断是否有极值;(Ⅱ)若对任意的x>1,恒有ln(x﹣1)+k+1≤kx成立,求k的取值范围;(Ⅲ)证明:(n∈N+,n≥2).福建省泉州五中2015届高考数学模拟试卷(文科)(5月份)参考答案与试题解析一.选择题:本大题共12小题,每小题...