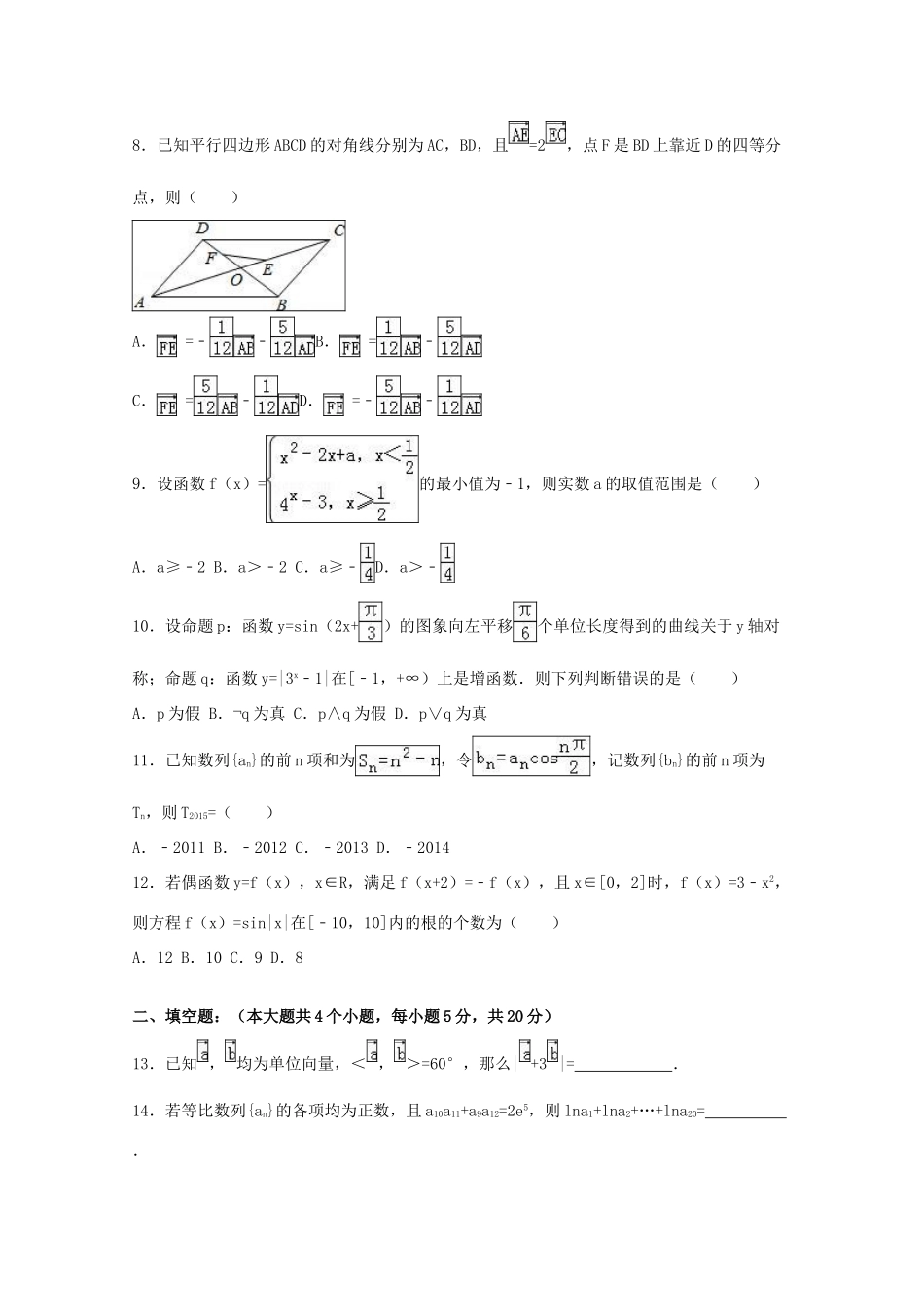
2015-2016学年福建省厦门六中高三(上)期中数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合A={x|﹣1<x<4},B={﹣1,1,2,4},则A∩B=()A.{1,2}B.{﹣1,4}C.{﹣1,2}D.{2,4}2.在复平面内,复数(4+5i)i(i为虚数单位)的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.若,为平面向量,则“=”是“||=||”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.曲线y=ax3+bx﹣1在点(1,f(1))处的切线方程为y=x,则b﹣a=()A.﹣3B.2C.3D.45.设a=log3,b=()0.3,c=log2(log2),则()A.b<c<aB.a<b<cC.c<a<bD.a<c<b6.已知数列{an}满足a1=1,an﹣1=2an(n≥2,n∈N+),则数列{an}的前6项和为()A.63B.127C.D.7.函数的图象如图所示,•=()A.8B.﹣8C.D.8.已知平行四边形ABCD的对角线分别为AC,BD,且=2,点F是BD上靠近D的四等分点,则()A.=﹣﹣B.=﹣C.=﹣D.=﹣﹣9.设函数f(x)=的最小值为﹣1,则实数a的取值范围是()A.a≥﹣2B.a>﹣2C.a≥﹣D.a>﹣10.设命题p:函数y=sin(2x+)的图象向左平移个单位长度得到的曲线关于y轴对称;命题q:函数y=|3x﹣1|在[﹣1,+∞)上是增函数.则下列判断错误的是()A.p为假B.¬q为真C.p∧q为假D.p∨q为真11.已知数列{an}的前n项和为,令,记数列{bn}的前n项为Tn,则T2015=()A.﹣2011B.﹣2012C.﹣2013D.﹣201412.若偶函数y=f(x),x∈R,满足f(x+2)=﹣f(x),且x∈[0,2]时,f(x)=3﹣x2,则方程f(x)=sin|x|在[﹣10,10]内的根的个数为()A.12B.10C.9D.8二、填空题:(本大题共4个小题,每小题5分,共20分)13.已知,均为单位向量,<,>=60°,那么|+3|=.14.若等比数列{an}的各项均为正数,且a10a11+a9a12=2e5,则lna1+lna2+…+lna20=.15.北京2008年第29届奥运会开幕式上举行升旗仪式,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为米(如图所示),则旗杆的高度为米.16.已知函数,.若∀x1∈[1,2],∃x2∈[﹣1,1]使f(x1)≥g(x2),则实数m的取值范围是.三、解答题(本题共6小题,共74分.)17.(选修4﹣4:坐标系与参数方程)已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)18.已知Sn为等差数列{an}的前n项和,且a2=4,S4=20.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设,求数列{bn}的前n项和.19.已知函数f(x)=cos2(x+),g(x)=1+sin2x.(1)设x0是函数y=f(x)的一个零点,求g(x0)的值;(2)求函数h(x)=f(x)+g(x)的单调递增区间.20.在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.(Ⅰ)求角A的大小;(Ⅱ)若△ABC的面积S=5,b=5,求sinBsinC的值.21.已知中心在原点,焦点在x轴上的椭圆C的离心率为,且经过点M.(Ⅰ)求椭圆C的方程;(Ⅱ)是否存过点P(2,1)的直线l1与椭圆C相交于不同的两点A,B,满足?若存在,求出直线l1的方程;若不存在,请说明理由.22.设函数f(x)=ax﹣lnx,g(x)=ex﹣ax,其中a为正实数.(l)若x=0是函数g(x)的极值点,讨论函数f(x)的单调性;(2)若f(x)在(1,+∞)上无最小值,且g(x)在(1,+∞)上是单调增函数,求a的取值范围;并由此判断曲线g(x)与曲线y=ax2﹣ax在(1,+∞)交点个数.2015-2016学年福建省厦门六中高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合A={x|﹣1<x<4},B={﹣1,1,2,4},则A∩B=()A.{1,2}B.{﹣1,4}C.{﹣1,2}D.{2,4}【考点】交集及其运算.【分析】由A与B,求出两集合的交集即可.【解答】解: A={x|﹣1...