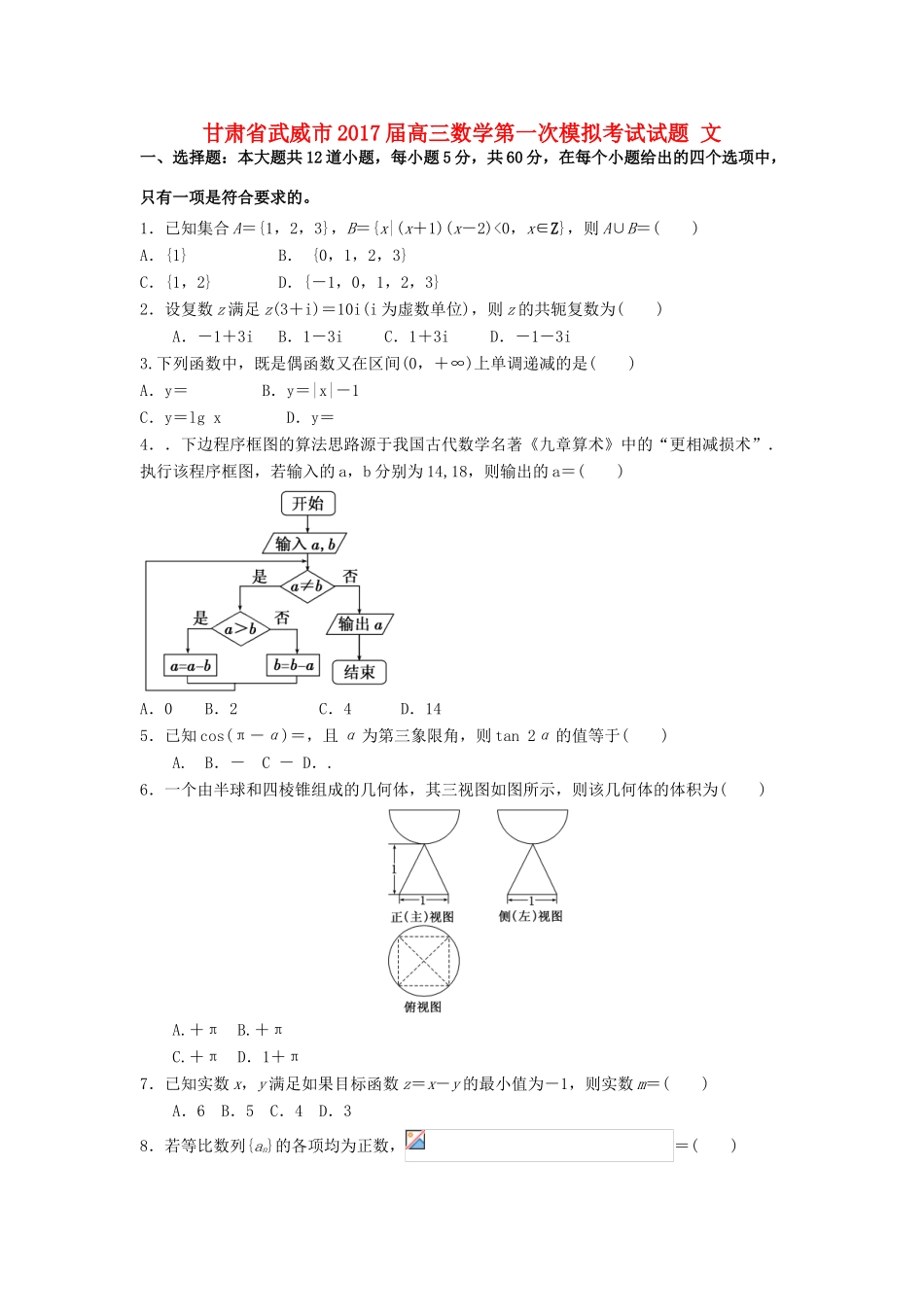
甘肃省武威市2017届高三数学第一次模拟考试试题文一、选择题:本大题共12道小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合要求的。1.已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=()A.{1}B.{0,1,2,3}C.{1,2}D.{-1,0,1,2,3}2.设复数z满足z(3+i)=10i(i为虚数单位),则z的共轭复数为()A.-1+3iB.1-3iC.1+3iD.-1-3i3.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是()A.y=B.y=|x|-1C.y=lgxD.y=4..下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0B.2C.4D.145.已知cos(π-α)=,且α为第三象限角,则tan2α的值等于()A.B.-C-D..6.一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为()A.+πB.+πC.+πD.1+π7.已知实数x,y满足如果目标函数z=x-y的最小值为-1,则实数m=()A.6B.5C.4D.38.若等比数列{an}的各项均为正数,=()A.B.C.D.9.若函数f(x)=sin(ω>0)的图象相邻两个对称中心之间的距离为,则f(x)的一个单调递增区间为()A.B.C.D.10.过抛物线(p>0)的焦点F且倾斜角为120°的直线l与抛物线在第一、四象限分别交于A,B两点,则的值等于()A.B.C.D.11.若圆上有且只有两个点到直线4x-3y=2的距离等于1,则半径r的取值范围是()A.(4,6)B.[4,6]C.[4,6)D.(4,6]12.若不等式2xlnx≥-x2+ax-3恒成立,则实数a的取值范围是()A.(-∞,0)B.(-∞,4]C.(0,+∞)D.[4,+∞)二.填空题:本大题共4小题,每小题5分,共20分.13.已知m∈R,向量a=(m,1),b=(2,-6),且a⊥b,则|a-b|=________.14.对于下列表格所示的五个散点,已知求得的线性回归直线方程为y=0.8x-155.x197198201204205y1367m则实数m的值为________..15.在长为12厘米的线段AB上任取一点C,现以线段AC,BC为邻边作一矩形,则该矩形的面积大于20cm2的概率为____________.16..如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本题满分12分)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.①求C;②若c=,△ABC的面积为,求△ABC的周长.18.(本题满分12分)根据世行2013年新标准,人均GDP低于1035美元为低收入国家;人均GDP为1035~4085美元为中等偏下收入国家;人均GDP为4085~12616美元为中等偏上收入国家;人均GDP不低于12616美元为高收入国家.某城市有5个行政区,各区人口占该城市人口比例及人均GDP如下表:行政区区人口占城市人口比例区人均GDP(单位:美元)A25%8000B30%4000C15%6000D10%3000E20%10000(1)判断该城市人均GDP是否达到中等偏上收入国家标准;(2)现从该城市5个行政区中随机抽取2个,求抽到的2个行政区人均GDP都达到中等偏上收入国家标准的概率.19.(本题满分12分)如图,几何体EFABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.(1)求证:AC⊥FB;(2)求几何体EFABCD的体积.20.(本题满分12分)已知焦点在y轴上的椭圆E的中心是原点O,离心率等于,以椭圆E的长轴和短轴为对角线的四边形的周长为4.直线l:y=kx+m与y轴交于点P,与椭圆E相交于A,B两个点.(1)求椭圆E的方程;(2)若,求m2的取值范围.21.(本题满分12分)已知函数(1)讨论的单调性;(2)当有最大值,且最大值大于2-2时,求的取值范围.选考题(请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题评分。)22.(本题满分10分)(选修4-4):坐标系与参数方程在直角坐标系xOy中,直线l的参数方程为(t为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=4sinθ-2cosθ.(1)求直线l的普通方程与曲线C的直角坐标方程;(2)...