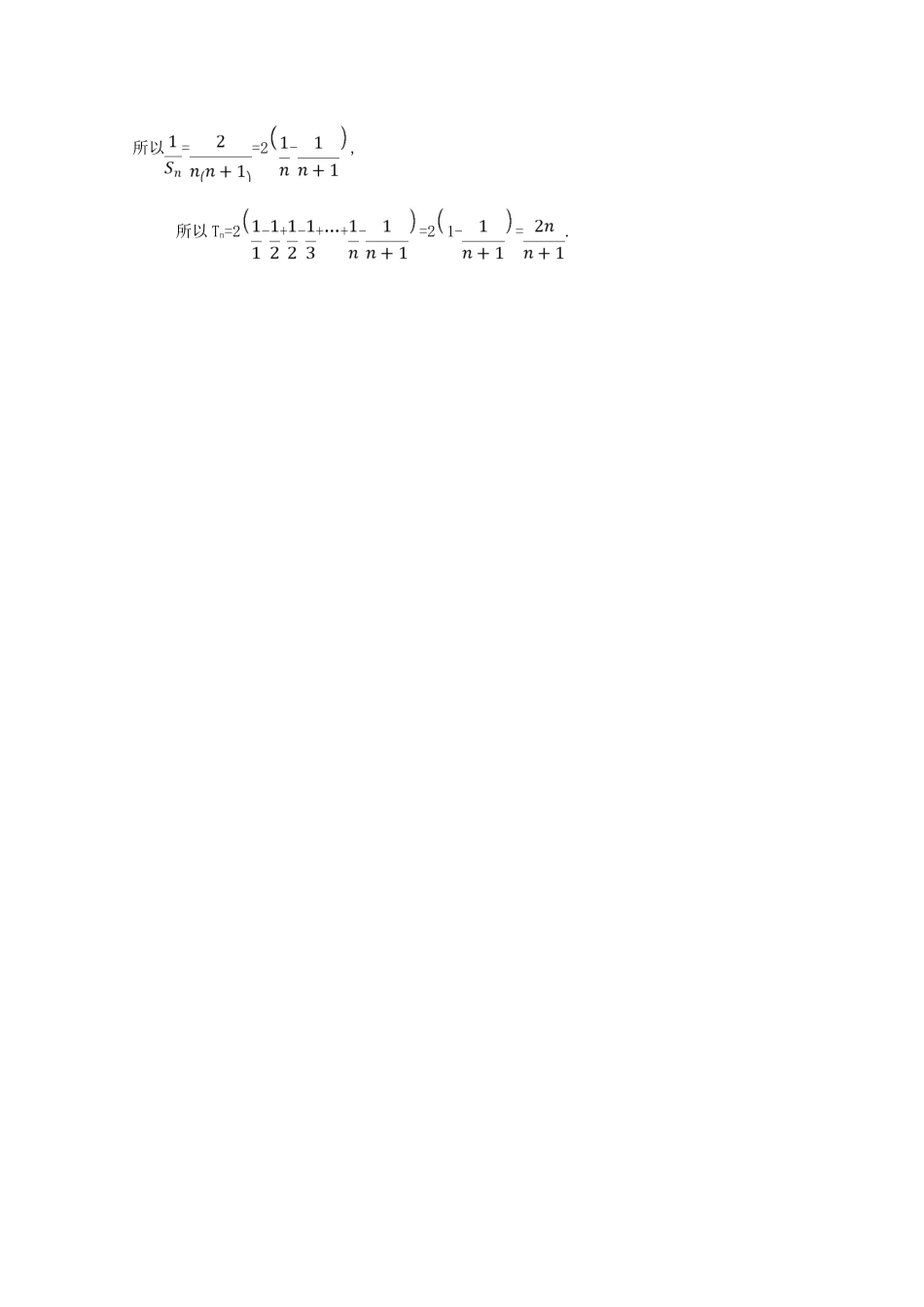大题规范满分练(三)数列综合问题1.(2018·全国卷Ⅱ)记Sn为等差数列{an}的前n项和,已知a1=-7,S3=-15.(1)求{an}的通项公式.(2)求Sn,并求Sn的最小值.【解析】(1)设等差数列{an}的公差为d,由题意得3a1+3d=-15.由a1=-7得d=2.所以{an}的通项公式为an=2n-9.(2)由(1)得Sn=n2-8n=(n-4)2-16.所以当n=4时,Sn取得最小值,最小值为-16.2.已知在正项等比数列{an}中,a1与a3分别是方程x2-5x+4=0的两根.(1)求数列{an}的通项公式.(2)若数列{bn}是递增数列,其前n项和为Sn,且bn=log2an+1,求数列的前n项和Tn.【解析】(1)设等比数列{an}的公比为q,依题意得或若因为an>0,则q=2,所以an=1×2n-1=2n-1.若,因为an>0,则q=,所以an=4×n-1=23-n.(2)因为数列{bn}是递增数列,bn=log2an+1,所以由(1)知an=2n-1,bn=log2an+1=n-1+1=n,所以{bn}是以1为首项,1为公差的等差数列,所以Sn==.所以==2-,所以Tn=2-+-+…+-=21-=.