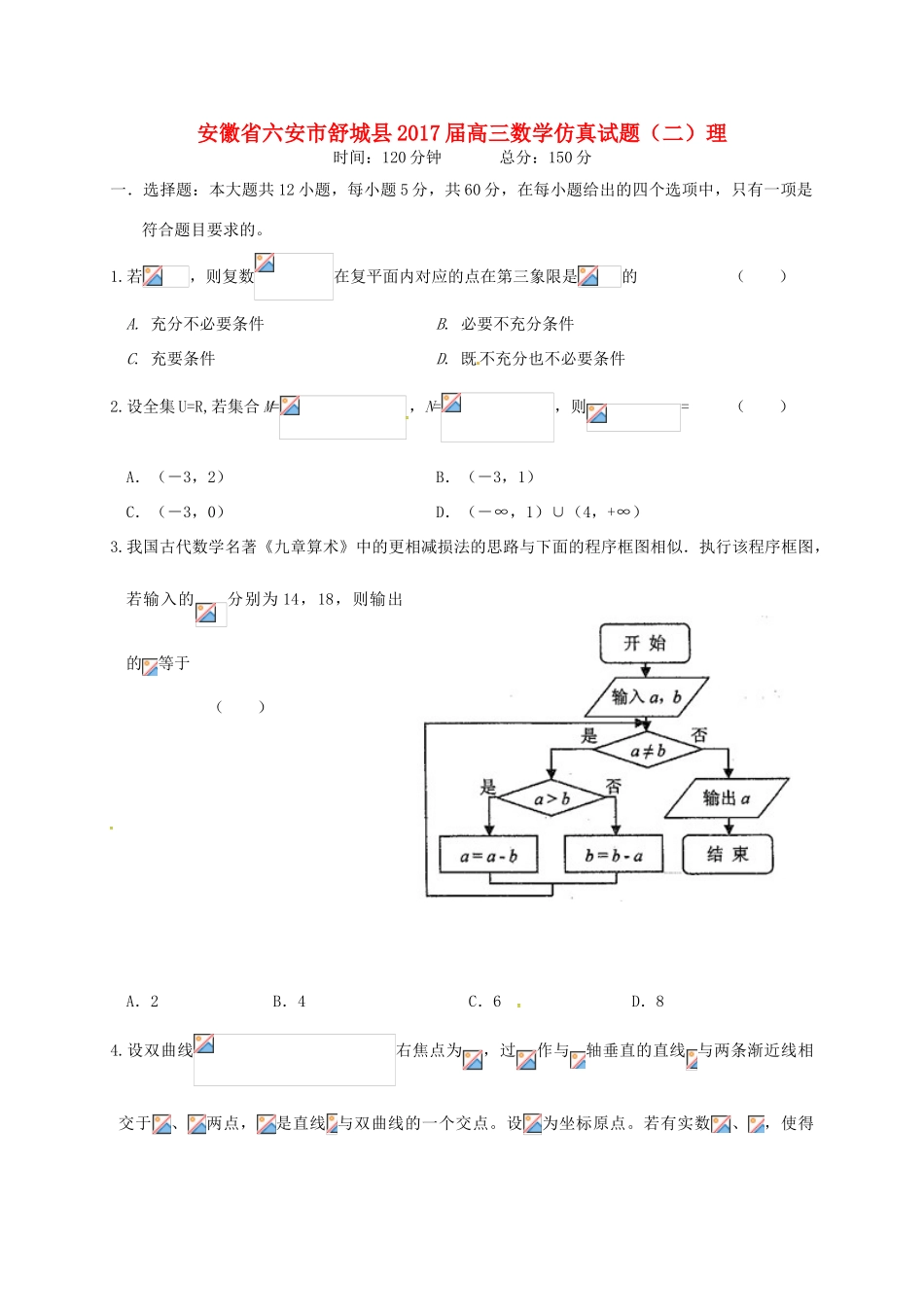
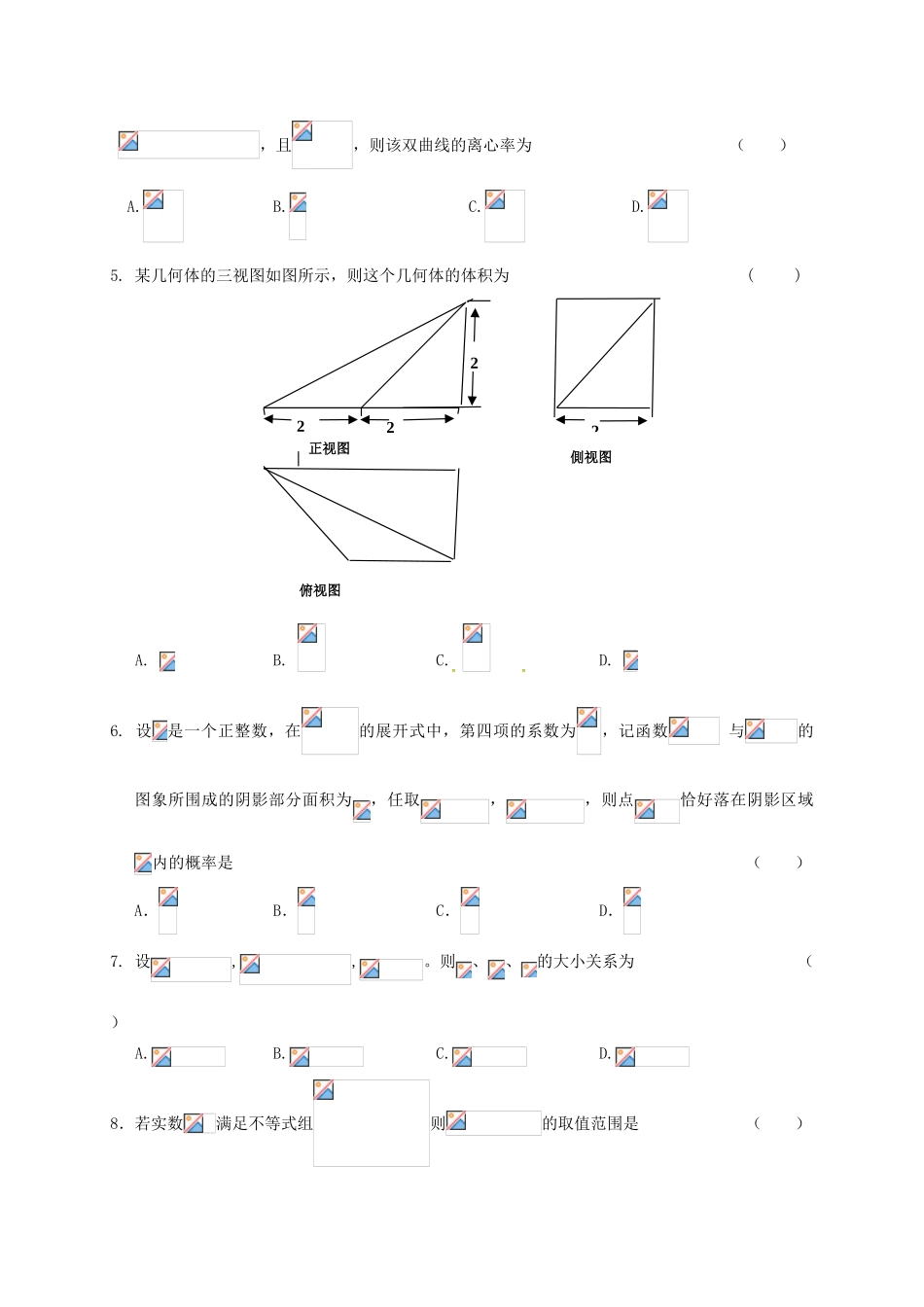
安徽省六安市舒城县2017届高三数学仿真试题(二)理时间:120分钟总分:150分一.选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。1.若,则复数在复平面内对应的点在第三象限是的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.设全集U=R,若集合M=,N=,则=()A.(-3,2)B.(-3,1)C.(-3,0)D.(-∞,1)∪(4,+∞)3.我国古代数学名著《九章算术》中的更相减损法的思路与下面的程序框图相似.执行该程序框图,若输入的分别为14,18,则输出的等于()A.2B.4C.6D.84.设双曲线右焦点为,过作与轴垂直的直线与两条渐近线相交于、两点,是直线与双曲线的一个交点。设为坐标原点。若有实数、,使得,且,则该双曲线的离心率为()A.B.C.D.5.某几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.6.设是一个正整数,在的展开式中,第四项的系数为,记函数与的图象所围成的阴影部分面积为,任取,,则点恰好落在阴影区域内的概率是()A.B.C.D.7.设,,。则、、的大小关系为()A.B.C.D.8.若实数满足不等式组则的取值范围是()正视图2222|俯视图側视图A.B.C.D.9.设函数且。则()A.B.C.D.10.设曲线的一条对称轴为,则曲线的一个对称点为()A.B.C.D.11.当取遍全体实数时,直线所围成的图形的面积是()A.B.C.D.12.把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为()A.l0cmB.10cmC.10cmD.30cm二、填空题:本大题共4小题,每小题5分,共20分。13.若三个非零实数:、、成等比数列,则其公比。14.如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是,向右的概率是,则第6秒时到达B(4,2)点的概率为。霍中高三理数第1页(共6页)15.已知、、三个实数成等差数列,则直线与抛物线的相交弦中点的轨迹方程是。16.设为三角形的重心,且,若,则实数的值为.三、解答题:解答应写出文字说明,证明过程或演算步骤。17.(本小题满分12分)已知数列满足:(1)求数列的通项公式;(2)若,求数列的最大项。18.(本小题满分12分)如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.(1)求证:BD∥平面FGH;(2)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.19.(本小题满分12分)某班级数学兴趣小组为了研究人的脚的大小与身高的关系,随机抽测了20位同学,得到如下数据:序号12345678910身高x(厘米)192164172177176159171166182166脚长y(码)48384043443740394639序号11121314151617181920身高x(厘米)169178167174168179165170162170脚长y(码)43414043404438423941(Ⅰ)请根据“序号为5的倍数”的几组数据,求出y关于x的线性回归方程(Ⅱ)若“身高大于175厘米”为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”为“大码”,“脚长小于等于42码”的为“非大码”。请根据上表数据完成2×2列联表:并根据列联表中数据说明能有多大的可靠性认为脚的大小与身高之间有关系?(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,求:抽到“无效序号(超过20号)”的概率。附表及公式:0.150.100.050.0250.0100.0050.0012.0722.7063.8415.0246.6357.87910.828.20.(本小题满分12分)如图,O为坐标原点,点F为抛物线C1:的焦点,且舒中高三理数第3页(共6页)抛物线C1上点M处的切线与圆C2:相切于点Q.(Ⅰ)当直线MQ的方程为时,求抛物线C1的方程;(Ⅱ)当正数p变化时,记S1,S2分别为△FMQ,△FOQ的面积,求的最小值.21.(本小题满分12分)设函数(是自然对数的底数).(1)若,求函数的单调区间;(2)若在内无极值,求的取值范围;(3)设,求证:。M请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号22.(本小题满分10分)选修4-4:坐标系与参数方程极坐标系...