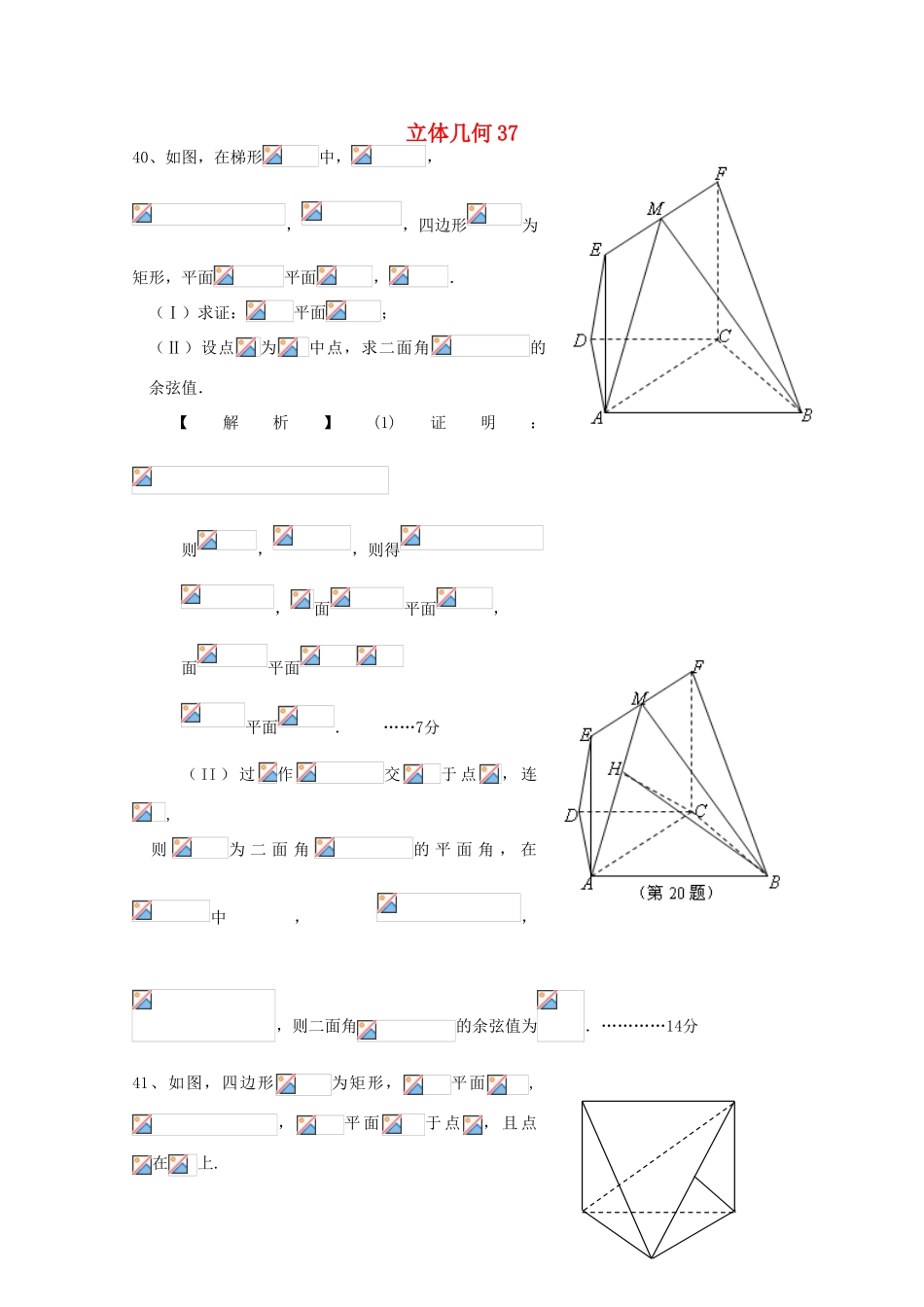
立体几何3740、如图,在梯形中,,,,四边形为矩形,平面平面,.(Ⅰ)求证:平面;(Ⅱ)设点为中点,求二面角的余弦值.【解析】(1)证明:则,,则得,面平面,面平面平面.……7分(II)过作交于点,连,则为二面角的平面角,在中,,,则二面角的余弦值为.…………14分41、如图,四边形为矩形,平面,,平面于点,且点在上.(Ⅰ)求证:;(Ⅱ)求四棱锥的体积;(Ⅲ)设点在线段上,且,试在线段上确定一点,使得平面.(Ⅱ)作,因为面平面,所以面因为,,所以…………………………6分…………………………………8分(Ⅲ)因为,平面于点,所以是的中点设是的中点,连接…………………………………………………10分所以∥∥因为,所以∥面,则点就是点…………………12分42、如图,在四棱锥中,侧棱底面,底面为矩形,,为的上一点,且.(Ⅰ)若F为PE的中点,求证:平面AEC;(Ⅱ)求三棱锥的体积.APCBDE43、如图在正三棱锥P-ABC中,侧棱长为3,底面边长为2,E为BC的中点,(1)求证:BC⊥平面PAB(2)求点C到平面PAB的距离【解析】证明(1)E为BC的中点,又为正三棱锥平面……6分(2)设点C到平面PAB的距离为。则…………10分…………………12分44、如图,三棱锥中,底面,,,为的中点,为的中点,点在上,且.(1)求证:平面;(2)求证:平面;(3)求三棱锥的体积.(2)取的中点,的中点,连接,∵为中点,,∴.……………7分∵平面平面,∴平面.…………8分同理可证:平面.又,∴平面平面.…………9分∵平面,∴平面.…………10分(3)由(1)可知平面又由已知可得.…………12分∴所以三棱锥的体积为.…………14分45、在四棱锥中,底面是菱形,.(Ⅰ)若,求证:平面;(Ⅱ)若平面平面,求证:;(Ⅲ)在棱上是否存在点(异于点)使得∥平面,若存在,求的值;若不存在,说明理由.【解析】(Ⅰ)证明:因为底面是菱形46、如图所示,圆柱的高为2,底面半径为,AE、DF是圆柱的两条母线,过作圆柱的截面交下底面于.(1)求证:;(2)若四边形ABCD是正方形,求证;(3)在(2)的条件下,求四棱锥的体积.【解析】(1)证明:在圆柱中:上底面//下底面,且上底面∩截面ABCD=,下底面∩截面ABCD=//……………………………………………………………………….2分又AE、DF是圆柱的两条母线,是平行四边形,所以,又//…………………………………………………………………….5分(2)AE是圆柱的母线,下底面,又下底面,…………………………….7分又截面ABCD是正方形,所以⊥,又⊥面,又面,……………………………9分(3)因为母线垂直于底面,所以是三棱锥的高……………………10分,EO就是四棱锥的高……………………10分