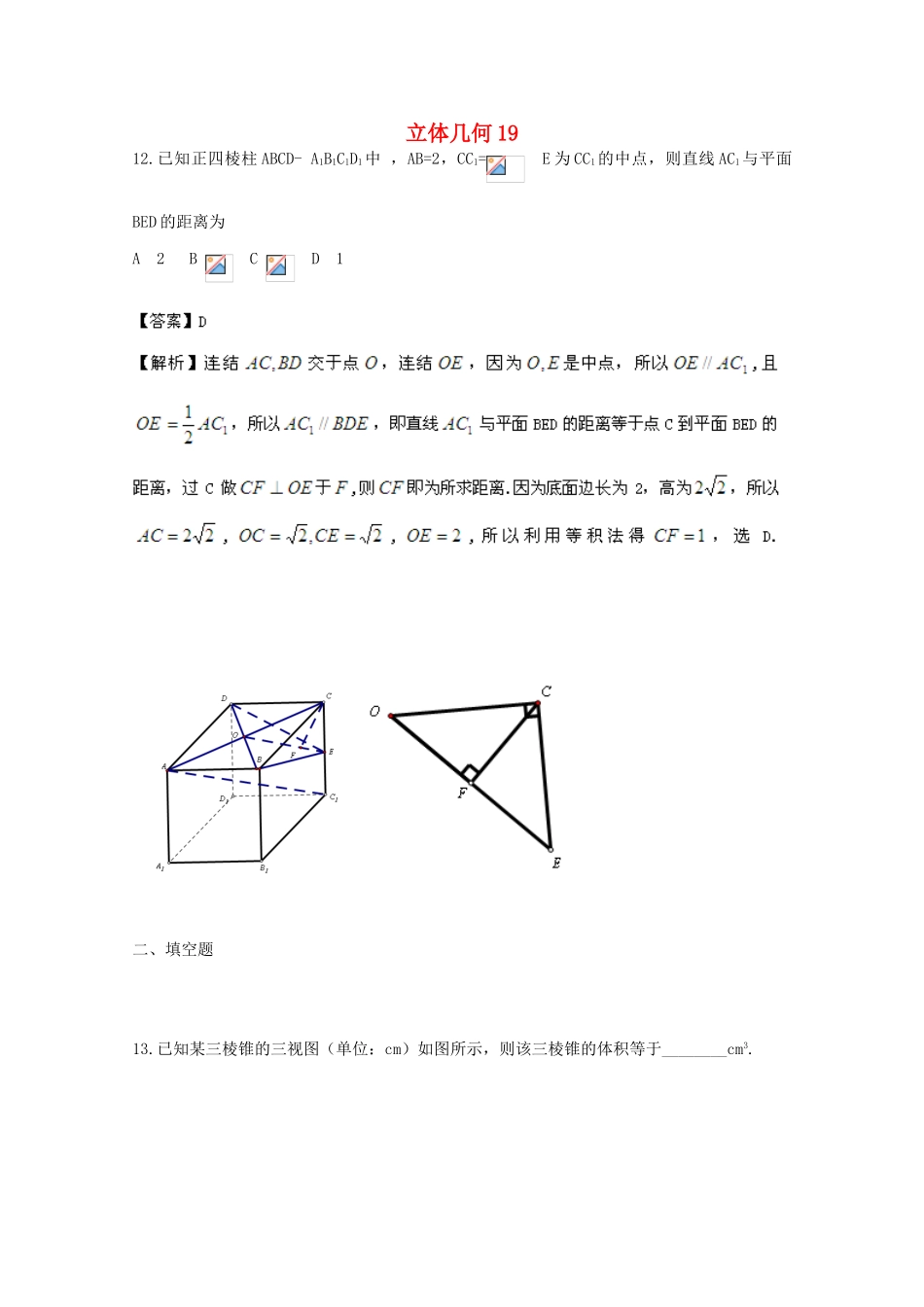
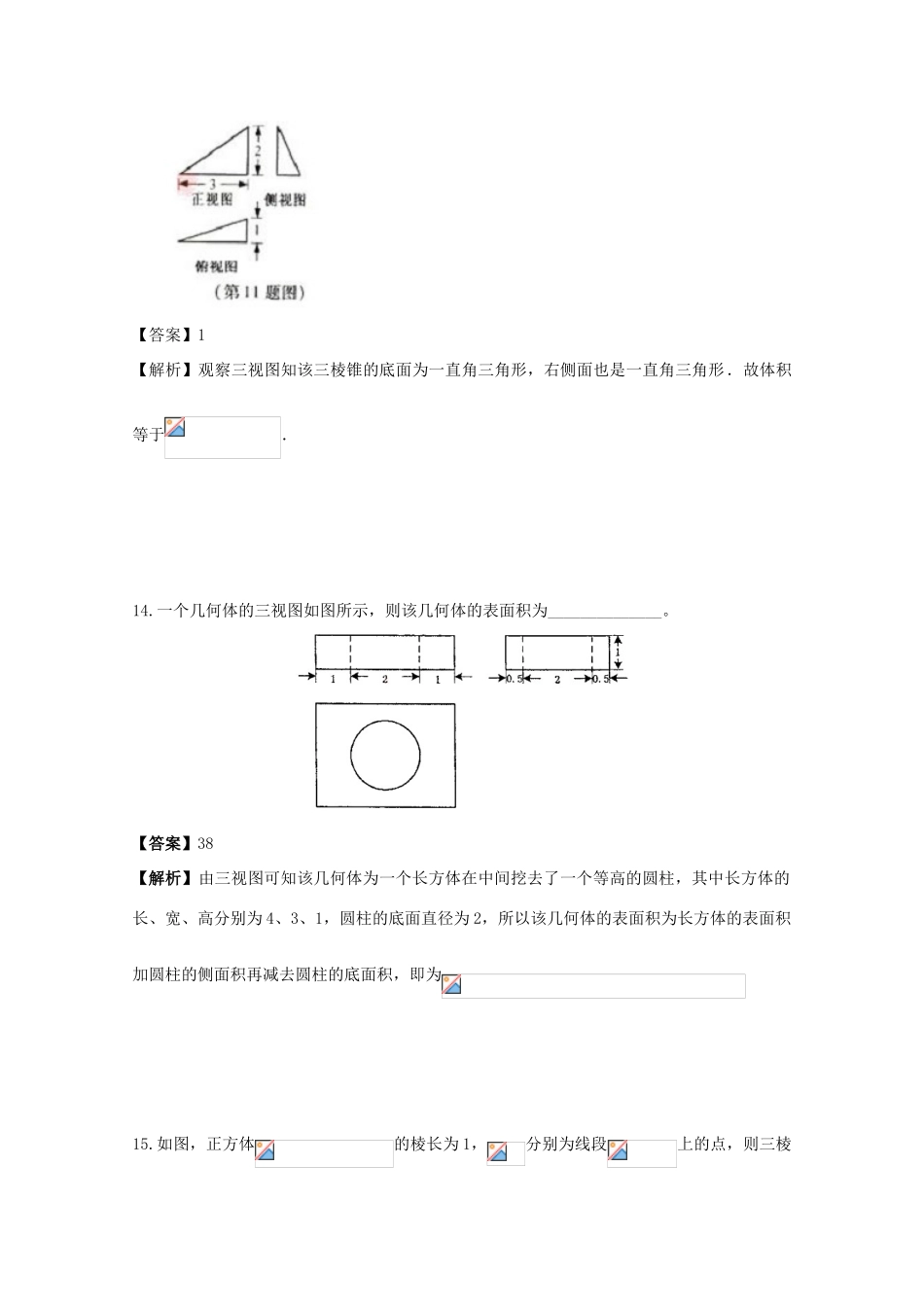
立体几何1912.已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=E为CC1的中点,则直线AC1与平面BED的距离为A2BCD1二、填空题13.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于________cm3.【答案】1【解析】观察三视图知该三棱锥的底面为一直角三角形,右侧面也是一直角三角形.故体积等于.14.一个几何体的三视图如图所示,则该几何体的表面积为______________。【答案】38【解析】由三视图可知该几何体为一个长方体在中间挖去了一个等高的圆柱,其中长方体的长、宽、高分别为4、3、1,圆柱的底面直径为2,所以该几何体的表面积为长方体的表面积加圆柱的侧面积再减去圆柱的底面积,即为15.如图,正方体的棱长为1,分别为线段上的点,则三棱锥的体积为____________.18.【2012高考真题辽宁理16】已知正三棱锥ABC,点P,A,B,C都在半径为的求面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为________。【答案】【解析】因为在正三棱锥ABC中,PA,PB,PC两两互相垂直,所以可以把该正三棱锥看作为一个正方体的一部分,(如图所示),此正方体内接于球,正方体的体对角线为球的直径,球心为正方体对角线的中点。球心到截面ABC的距离为球的半径减去正三棱锥ABC在面ABC上的高。已知球的半径为,所以正方体的棱长为2,可求得正三棱锥ABC在面ABC上的高为,所以球心到截面ABC的距离为16.若一个圆锥的侧面展开图是面积为的半圆面,则该圆锥的体积为。20.【2012高考真题上海理14】如图,与是四面体中互相垂直的棱,,若,且,其中、为常数,则四面体的体积的最大值是。【答案】。【解析】过点A做AE⊥BC,垂足为E,连接DE,由AD⊥BC可知,BC⊥平面ADE,所以=,当AB=BD=AC=DC=a时,四面体ABCD的体积最大。过E做EF⊥DA,垂足为点F,已知EA=ED,所以△ADE为等腰三角形,所以点E为AD的中点又,∴EF=,∴==,∴四面体ABCD体积的最大值=。17.如图,在长方体中,,,则四棱锥的体积为▲cm3.18.一个几何体的三视图如图所示(单位:m),则该几何体的体积为_________m3.31363223侧视图俯视图正视图