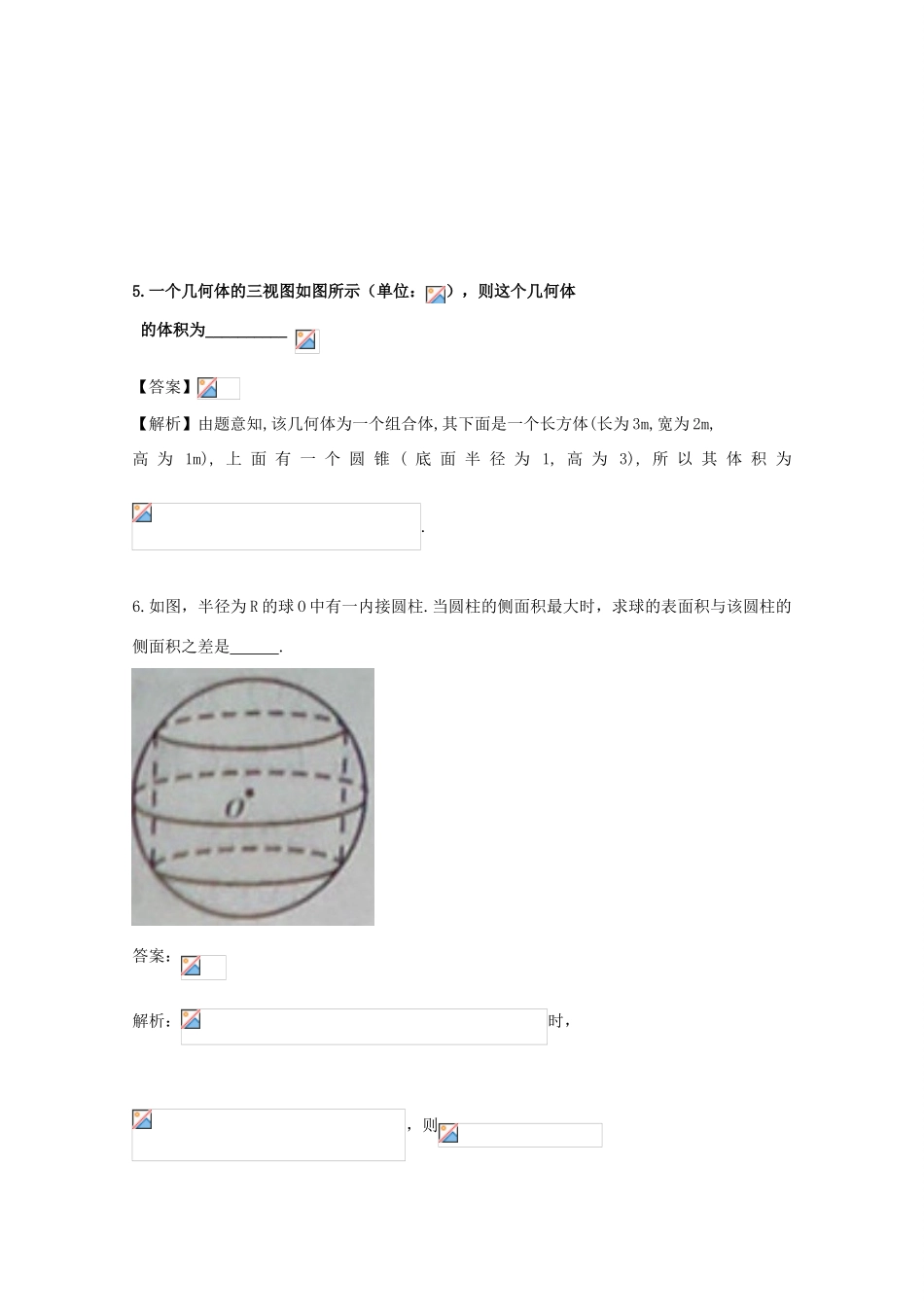
立体几何23一、选择题:1.已知平面截一球面得圆M,过圆心M且与成,二面角的平面截该球面得圆N,若该球的半径为4,圆M的面积为4,则圆N的面积为(A)(B)(c)(D)【答案】D【解析】:由圆的面积为得,,在故选D2.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A.8B.C.10D.【答案】C60°BAONM二、填空题:3.一个正三棱柱的侧棱长和底面边长相等,体积为,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是____________.4.已知矩形的顶点都在半径为4的球的球面上,且,则棱锥的体积为。5.一个几何体的三视图如图所示(单位:),则这个几何体的体积为__________【答案】【解析】由题意知,该几何体为一个组合体,其下面是一个长方体(长为3m,宽为2m,高为1m),上面有一个圆锥(底面半径为1,高为3),所以其体积为.6.如图,半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时,求球的表面积与该圆柱的侧面积之差是.答案:解析:时,,则7.己知点E、F分别在正方体ABCD-A1B2C3D4的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于.8.三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于______。【答案】9.若圆锥的侧面积为,底面积为,则该圆锥的体积为。【答案】;三、解答题1.在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE;(Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.【解析】(Ⅰ)连结AF,因为EF∥AB,FG∥BC,EF∩FG=F,所以平面EFG∥平面ABCD,又易证∽,所以,即,即,又M为AD的中点,所以,又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM平面ABFE,FA平面ABFE,所以GM∥平面ABFE.2.如图:在,沿把折起,使(Ⅰ)证明:平面;(Ⅱ)设。【解析】:(Ⅰ)折起前,当。(Ⅱ)由及(Ⅰ)知两两垂直,不妨设为坐标原点,以轴建立如图所示的空间直角坐标系,易得夹角的余弦值为3.如图,在四面体中,平面⊥,⊥,=,∠=(Ⅰ)若=2,=2,求四边形的体积。(Ⅱ)若二面角--为,求异面直线与所成角的余弦值。设E为边AB的中点,则EF//BC,由⊥,知⊥,又由(Ⅰ)有DF⊥平面,故由三垂线定理知⊥,所以为二面角--的平面角,由题设知,设AD=a,则DF=ADsinCAD=在中,,从而因,故BD=AD=a.从而,在中,,又,从而在中,因FG=FH,由余弦定理得,故异面直线与所成角的余弦值为.