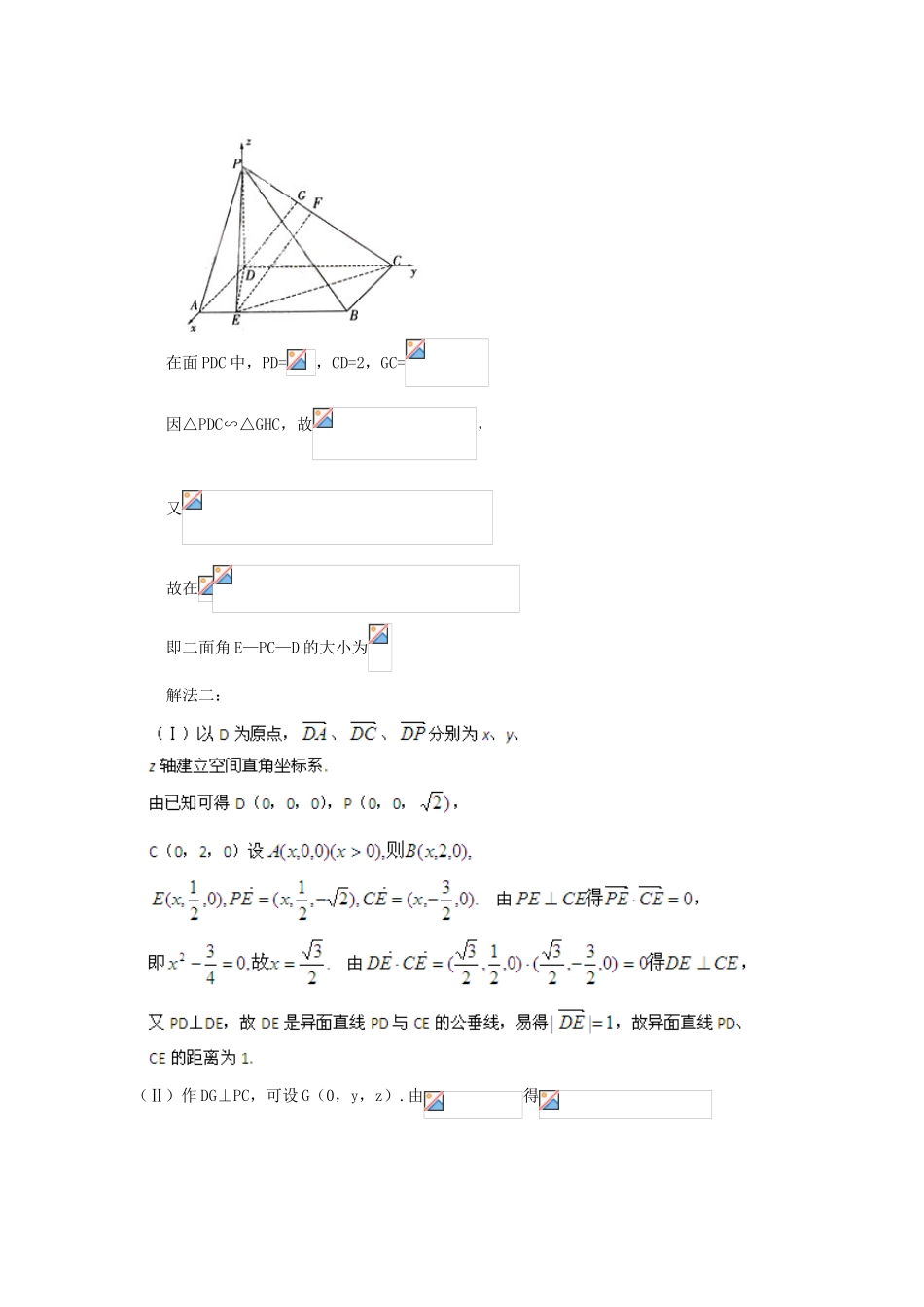
立体几何1715.如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知求(Ⅰ)异面直线PD与EC的距离;(Ⅱ)二面角E—PC—D的大小.在面PDC中,PD=,CD=2,GC=因△PDC∽△GHC,故,又故在即二面角E—PC—D的大小为解法二:(Ⅱ)作DG⊥PC,可设G(0,y,z).由得即作EF⊥PC于F,设F(0,m,n),则由,又由F在PC上得因故平面E—PC—D的平面角的大小为向量的夹角.故即二面角E—PC—D的大小为16.已知是函数的一个极值点,其中,(I)求与的关系式;(II)求的单调区间;(III)当时,函数的图象上任意一点的切线斜率恒大于3,求的取值范围.解(I)因为是函数的一个极值点,所以,即,所以(II)由(I)知,=当时,有,当变化时,与的变化如下表:100调调递减极小值单调递增极大值单调递减故有上表知,当时,在单调递减,在单调递增,在上单调递减.17.如图,已知长方体直线与平面所成的角为,垂直于,为的中点.(I)求异面直线与所成的角;(II)求平面与平面所成的二面角;(III)求点到平面的距离.解:在长方体中,以所在的直线为轴,以所在的直线为轴,所在的直线为轴建立如图示空间直角坐标系由已知可得,又平面,从而与平面所成的角为,又,,从而易得(I)因为所以=易知异面直线所成的角为