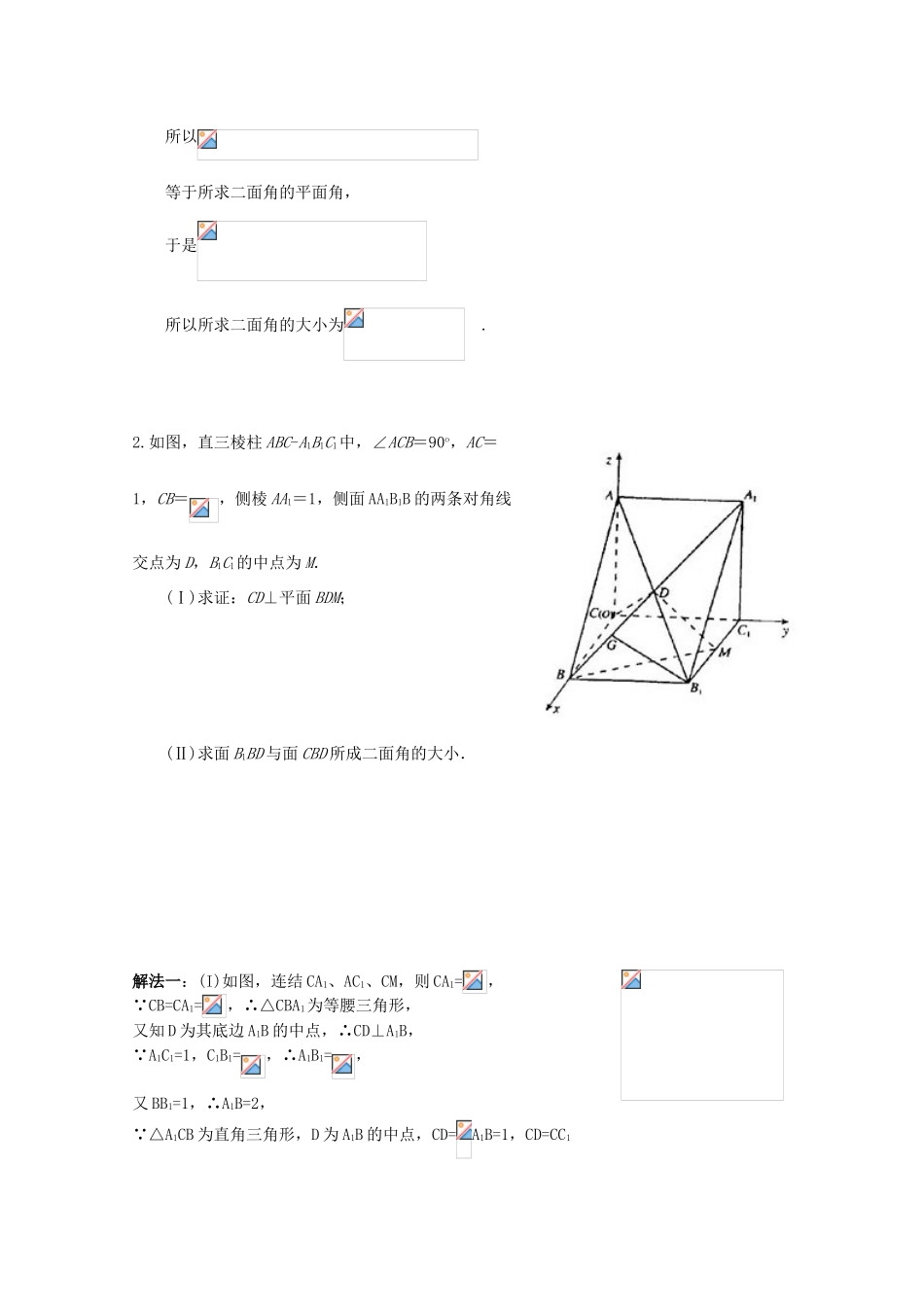
立体几何011.如图,已知四棱锥P—ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.(I)求点P到平面ABCD的距离,(II)求面APB与面CPB所成二面角的大小.(II)解法一:如图建立直角坐标系,其中O为坐标原点,x轴平行于DA..连结AG.又知由此得到:所以等于所求二面角的平面角,于是所以所求二面角的大小为.2.如图,直三棱柱ABC-A1B1C1中,∠ACB=90o,AC=1,CB=,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,B1C1的中点为M.(Ⅰ)求证:CD⊥平面BDM;(Ⅱ)求面B1BD与面CBD所成二面角的大小.解法一:(I)如图,连结CA1、AC1、CM,则CA1=,∵CB=CA1=,∴△CBA1为等腰三角形,又知D为其底边A1B的中点,∴CD⊥A1B,∵A1C1=1,C1B1=,∴A1B1=,又BB1=1,∴A1B=2,∵△A1CB为直角三角形,D为A1B的中点,CD=A1B=1,CD=CC1解法二:如图以C为原点建立坐标系(I):B(,0,0),B1(,1,0),A1(0,1,1),D(,,),M(,1,0),(,,),(,-1,-1),(0,,-),∴CD⊥A1B,CD⊥DM.因为A1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM(II):设BD中点为G,连结B1G,则G(-,,),∴,∴BD⊥B1G,又CD⊥BD,∴与的夹角等于所求二面角的平面角,cos所以所求二面角的大小为π-arccos3.如图,四棱锥的底面是边长为1的正方形,SD垂直于底面ABCD,(I)求证;(II)(II)求面ASD与面BSC所成二面角的大小;(III)设棱SA的中点为M,求异面直线DM与SB所成角的大小解析:(I)证明:如图1图1底面ABCD是正方形底面ABCDDC是SC在平面ABCD上的射影由三垂线定理得(II)解:底面ABCD,且ABCD为正方形可以把四棱锥补形为长方体,如图2面ASD与面BSC所成的二面角就是面与面所成的二面角,又为所求二面角的平面角在中,由勾股定理得在中,由勾股定理得即面ASD与面BSC所成的二面角为图2图3(III)解:如图3是等腰直角三角形又M是斜边SA的中点面ASD,SA是SB在面ASD上的射影由三垂线定理得异面直线DM与SB所成的角为