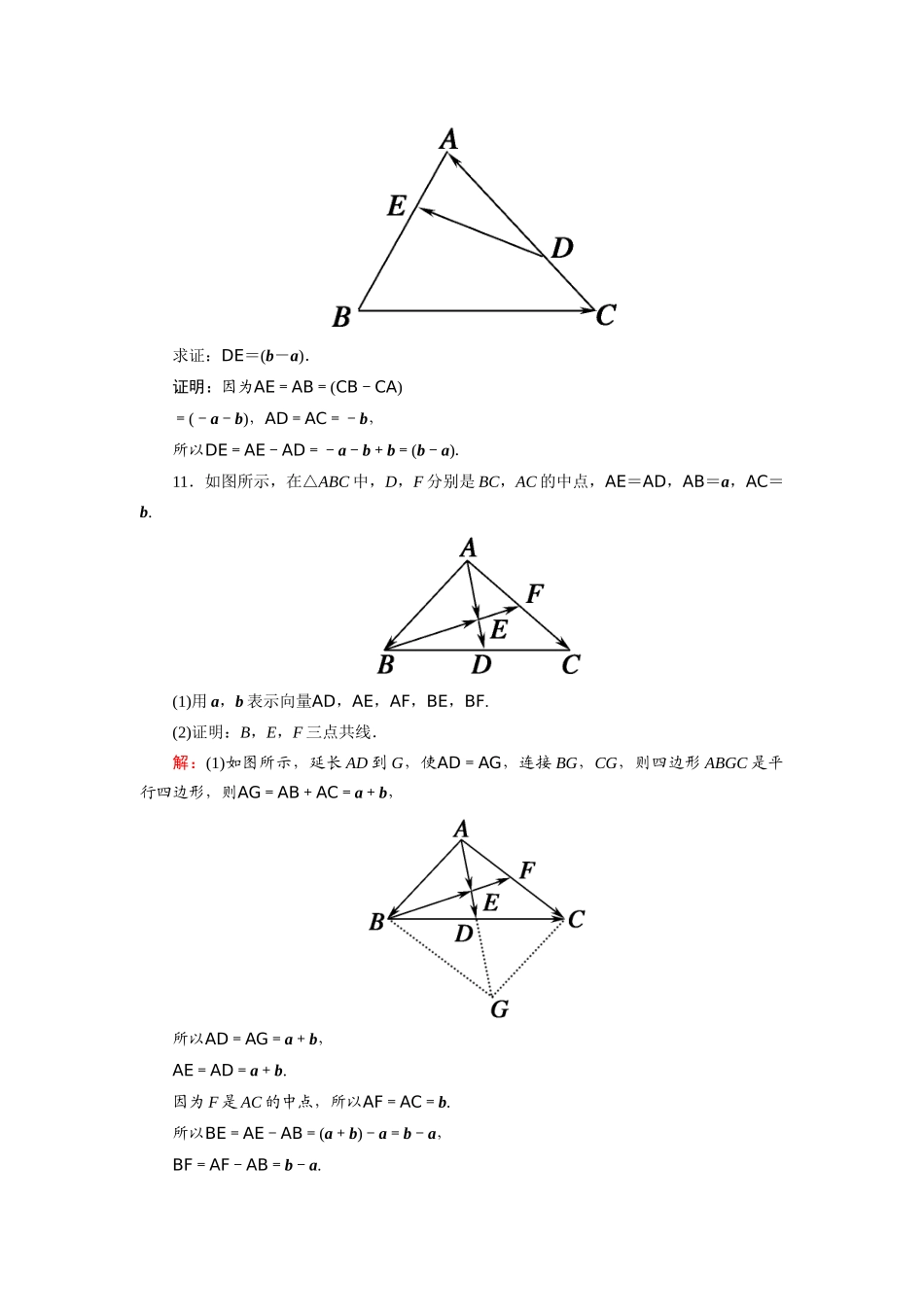
课时作业17向量数乘运算及其几何意义——基础巩固类——一、选择题1.-等于(A)A.a-b+2cB.5a-b+2cC.a+b+2cD.5a+b解析:-=(3a-2a)++(c+c)=a-b+2c,故选A.2.若5AB+3CD=0,且|AD|=|BC|,则四边形ABCD是(D)A.平行四边形B.菱形C.矩形D.等腰梯形解析:由5AB+3CD=0知,AB∥CD且|AB|≠|CD|,∴此四边形为梯形.又|AD|=|BC|,∴梯形ABCD为等腰梯形.3.在△ABC中,AB=c,AC=b.若点D满足BD=2DC,则AD=(A)A.b+cB.c-bC.b-cD.b+c解析:如图,AD=AB+BD=AB+BC=AB+(AC-AB)=c+(b-c)=b+c.4.已知向量a与b不共线,且AB=λa+b(λ∈R),AC=a+μb(μ∈R),则A、B、C三点共线应满足(D)A.λ+μ=2B.λ-μ=1C.λμ=-1D.λμ=1解析:若A,B,C三点共线,则AB=kAC(k∈R),即λa+b=k(a+μb),所以λa+b=ka+μkb,所以消去k得λμ=1,故选D.5.设D为△ABC所在平面内一点,BC=3CD,则(A)A.AD=-AB+ACB.AD=AB-ACC.AD=AB+ACD.AD=AB-AC解析:AD=AB+BD=AB+BC=AB+(AC-AB)=-AB+AC,选A.6.点P是△ABC所在平面内一点,若CB=λPA+PB,其中λ∈R,则点P一定在(B)A.△ABC内部B.AC边所在的直线上C.AB边所在的直线上D.BC边所在的直线上解析:∵CB=λPA+PB,∴CB-PB=λPA.∴CP=λPA.∴P、A、C三点共线.∴点P一定在AC边所在的直线上.二、填空题7.化简(a-b)-(2a+4b)+(2a+13b)=0.解析:(a-b)-(2a+4b)+(2a+13b)=a-b-a-b+a+b=(-+)a+(--+)b=0a+0b=0+0=0.8.设向量a与b不共线,若AB=3a+b,BC=a+mb,CD=2a-b,且A,C,D三点共线,则m=-3.解析:AC=AB+BC=4a+(m+1)b,CD=2a-b.∵a,b不共线,∴CD≠0,又A,C,D三点共线,∴AC=nCD(n∈R),即4a+(m+1)b=2na-nb,∴∴m=-3.9.如图所示,在▱ABCD中,AB=a,AD=b,AN=3NC,M为BC的中点,则MN=(b-a)(用a,b表示).解析:MN=MB+BA+AN=-BC+BA+AC=-AD-AB+(AB+AD)=-b-a+(a+b)=b-a=(b-a).三、解答题10.如图,在△ABC中,D、E分别为AC、AB边上的点,==,记BC=a,CA=b.求证:DE=(b-a).证明:因为AE=AB=(CB-CA)=(-a-b),AD=AC=-b,所以DE=AE-AD=-a-b+b=(b-a).11.如图所示,在△ABC中,D,F分别是BC,AC的中点,AE=AD,AB=a,AC=b.(1)用a,b表示向量AD,AE,AF,BE,BF.(2)证明:B,E,F三点共线.解:(1)如图所示,延长AD到G,使AD=AG,连接BG,CG,则四边形ABGC是平行四边形,则AG=AB+AC=a+b,所以AD=AG=a+b,AE=AD=a+b.因为F是AC的中点,所以AF=AC=b.所以BE=AE-AB=(a+b)-a=b-a,BF=AF-AB=b-a.(2)证明:由(1)可知BE=(b-2a),BF=(b-2a),所以BE=BF,即BE,BF是共线向量,且有公共点B,所以B,E,F三点共线.——能力提升类——12.已知△ABC和点M满足MA+MB+MC=0.若存在实数m使得AB+AC=mAM成立,则m=(B)A.2B.3C.4D.5解析:如图,在△ABC中,以BM,CM为邻边作平行四边形MBDC,依据平行四边形法则可得MC+MB=MD,又MA+MB+MC=0,则AM=MD,两向量有公共点M,则A,M,D三点共线,结合MD是平行四边形MBDC的对角线,可知M是△ABC的重心.以AB,AC为邻边作平行四边形ABFC,由向量加法的平行四边形法则,可得AB+AC=AF=2AE=2×AM=3AM,则AB+AC=3AM.13.已知点P在正三角形ABC所确定的平面上,且满足PA+PB+PC=AB,则△ABP的面积与△BCP的面积之比为(B)A.11B.12C.13D.14解析:∵PA+PB+PC=AB,∴PA+PC=AB-PB=AP,∴PC=2AP,即点P为线段AC的靠近点A的三等分点,∴△ABP的面积与△BCP的面积之比为12,故选B.14.如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若AB=mAM,AC=nAN,则m+n的值为2.解析:AO=(AB+AC)=AM+AN,∵M,O,N三点共线,∴+=1,∴m+n=2.15.已知e,f为两个不共线的向量,且四边形ABCD满足AB=e+2f,BC=-4e-f,CD=-5e-3f.(1)将AD用e,f表示;(2)证明:四边形ABCD为梯形.解:(1)AD=AB+BC+CD=(e+2f)+(-4e-f)+(-5e-3f)=(1-4-5)e+(2-1-3)f=-8e-2f.(2)证明:因为AD=-8e-2f=2(-4e-f)=2BC,所以AD与BC同向,且AD的模为BC模的2倍,所以在四边形ABCD中,AD∥BC,且AD≠BC,所以四边形ABCD是梯形.