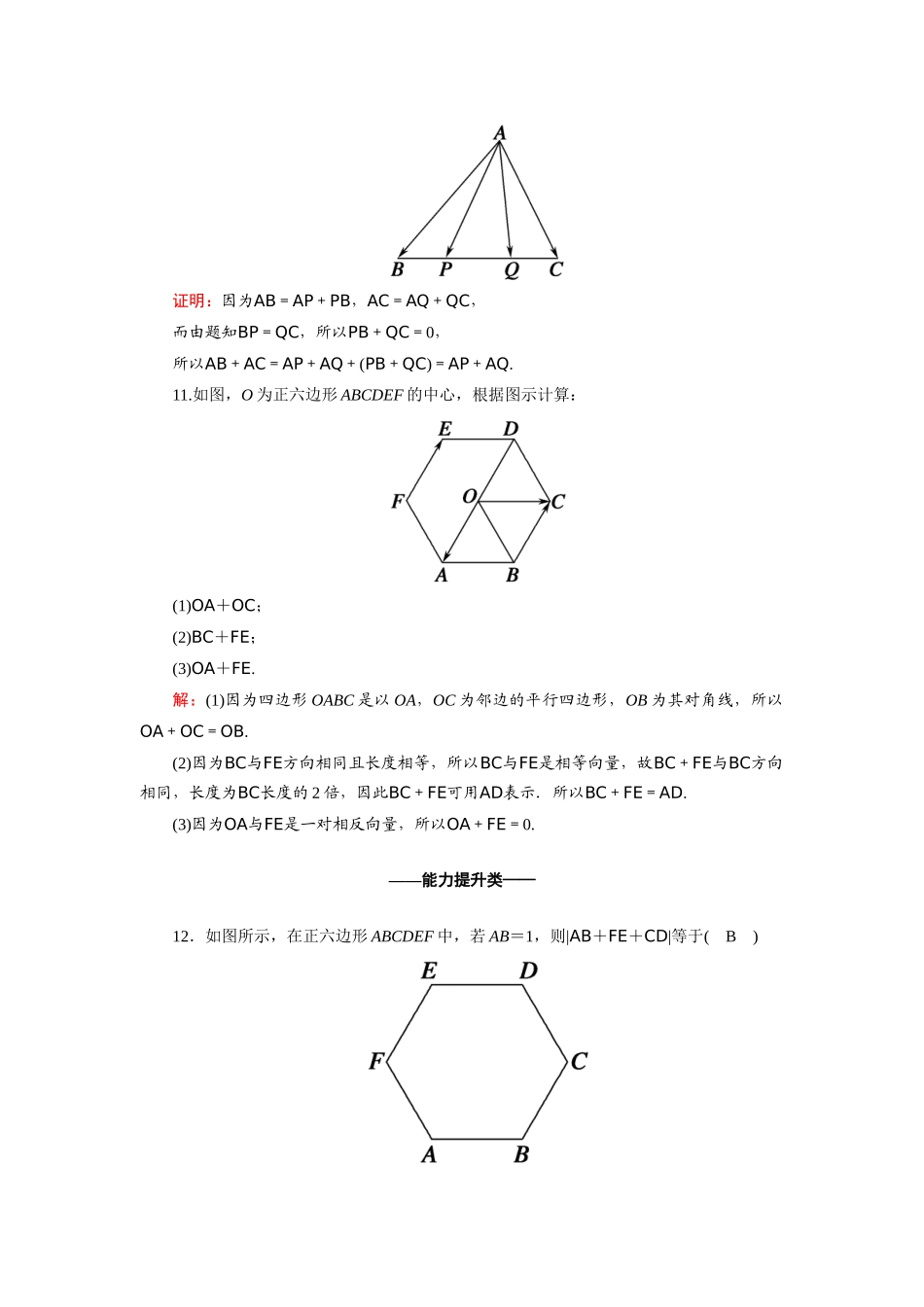
课时作业15向量加法运算及其几何意义——基础巩固类——一、选择题1.如图所示,在平行四边形ABCD中,BC+DC+BA等于(A)A.BCB.DBC.BDD.CB解析:BC+DC+BA=BC+(DC+BA)=BC+0=BC.故选A.2.下列等式错误的是(B)A.a+0=0+aB.AB+BC+AC=0C.AB+BD=ADD.AB+BO+OM+MB=AB解析:AB+BC+AC=AC+AC≠0.故选B.3.若向量a表示向东走1km,向量b表示向南走1km,则向量a+b表示(A)A.向东南走kmB.向东南走2kmC.向东北走kmD.向东北走2km解析:如图所示,a+b表示向东南方向走km.故选A.4.已知下列各式:①AB+BC+CA;②(AB+MB)+BO+OM;③OA+OC+BO+CO;④AB+CA+BD+DC.其中结果为0的个数是(B)A.1B.2C.3D.4解析:由向量加法的运算法则知①④的结果为0.故选B.5.在平行四边形ABCD中,若|BC+BA|=|BC+AB|,则四边形ABCD是(B)A.菱形B.矩形C.正方形D.不确定解析:依题意,平行四边形ABCD中,|BC+BA|=|BC+AB|,则平行四边形ABCD的两条对角线相等.故四边形ABCD为矩形.故选B.6.下列说法:①如果非零向量a与b的方向相同或相反,那么a+b的方向必与a,b之一的方向相同;②△ABC中,必有AB+BC+CA=0;③若AB+BC+CA=0,则A,B,C为一个三角形的三个顶点;④若a,b均为非零向量,则|a+b|与|a|+|b|一定相等.其中正确说法的个数为(B)A.0B.1C.2D.3解析:①错,若a+b=0时,方向是任意的;②正确;③错,A,B,C三点共线时也满足;④错,|a+b|≤|a|+|b|.二、填空题7.如图,在平行四边形ABCD中(1)AB+AD=AC;(2)AC+CD+DO=AO;(3)AB+AD+CD=AD.8.在菱形ABCD中,∠BAD=60°,|AB|=1,则|BC+CD|=1.解析:由题知△ABD为等边三角形,所以|BC+CD|=|BD|=|AB|=1.9.若a,b为非零向量,则下列叙述中使|a+b|=|a|+|b|成立的是①②.①a∥b且a,b方向相同;②a=b;③a=-b.三、解答题10.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:AB+AC=AP+AQ.证明:因为AB=AP+PB,AC=AQ+QC,而由题知BP=QC,所以PB+QC=0,所以AB+AC=AP+AQ+(PB+QC)=AP+AQ.11.如图,O为正六边形ABCDEF的中心,根据图示计算:(1)OA+OC;(2)BC+FE;(3)OA+FE.解:(1)因为四边形OABC是以OA,OC为邻边的平行四边形,OB为其对角线,所以OA+OC=OB.(2)因为BC与FE方向相同且长度相等,所以BC与FE是相等向量,故BC+FE与BC方向相同,长度为BC长度的2倍,因此BC+FE可用AD表示.所以BC+FE=AD.(3)因为OA与FE是一对相反向量,所以OA+FE=0.——能力提升类——12.如图所示,在正六边形ABCDEF中,若AB=1,则|AB+FE+CD|等于(B)A.1B.2C.3D.2解析:由正六边形知FE=BC,所以AB+FE+CD=AB+BC+CD=AD,所以|AB+FE+CD|=|AD|=2.故选B.13.已知|a|=8,|b|=5,则|a+b|的取值范围是[3,13].解析:||a|-|b||≤|a+b|≤|a|+|b|,即3≤|a+b|≤13.14.已知△ABC是正三角形,给出下列等式:①|AB+BC|=|BC+CA|;②|AC+CB|=|BA+BC|;③|AB+AC|=|CA+CB|;④|AB+BC+AC|=|CB+BA+CA|.其中正确的有①③④.(写出所有正确等式的序号)解析:AB+BC=AC,BC+CA=BA,而|AC|=|BA|,故①正确;|AC+CB|=|AB|≠|BA+BC|,故②不正确;画图(图略)可知③正确;|AB+BC+AC|=|AC+AC|,|CB+BA+CA|=|CA+CA|,故④正确.15.如图,已知D,E,F分别为△ABC的三边BC、AC、AB的中点.求证:AD+BE+CF=0.证明:由题意知:AD=AC+CD,BE=BC+CE,CF=CB+BF.由平面几何可知:EF=CD,BF=FA.∴AD+BE+CF=(AC+CD)+(BC+CE)+(CB+BF)=(AC+CD+CE+BF)+(BC+CB)=(AE+EC+CD+CE+BF)+0=AE+CD+BF=AE+EF+FA=0.