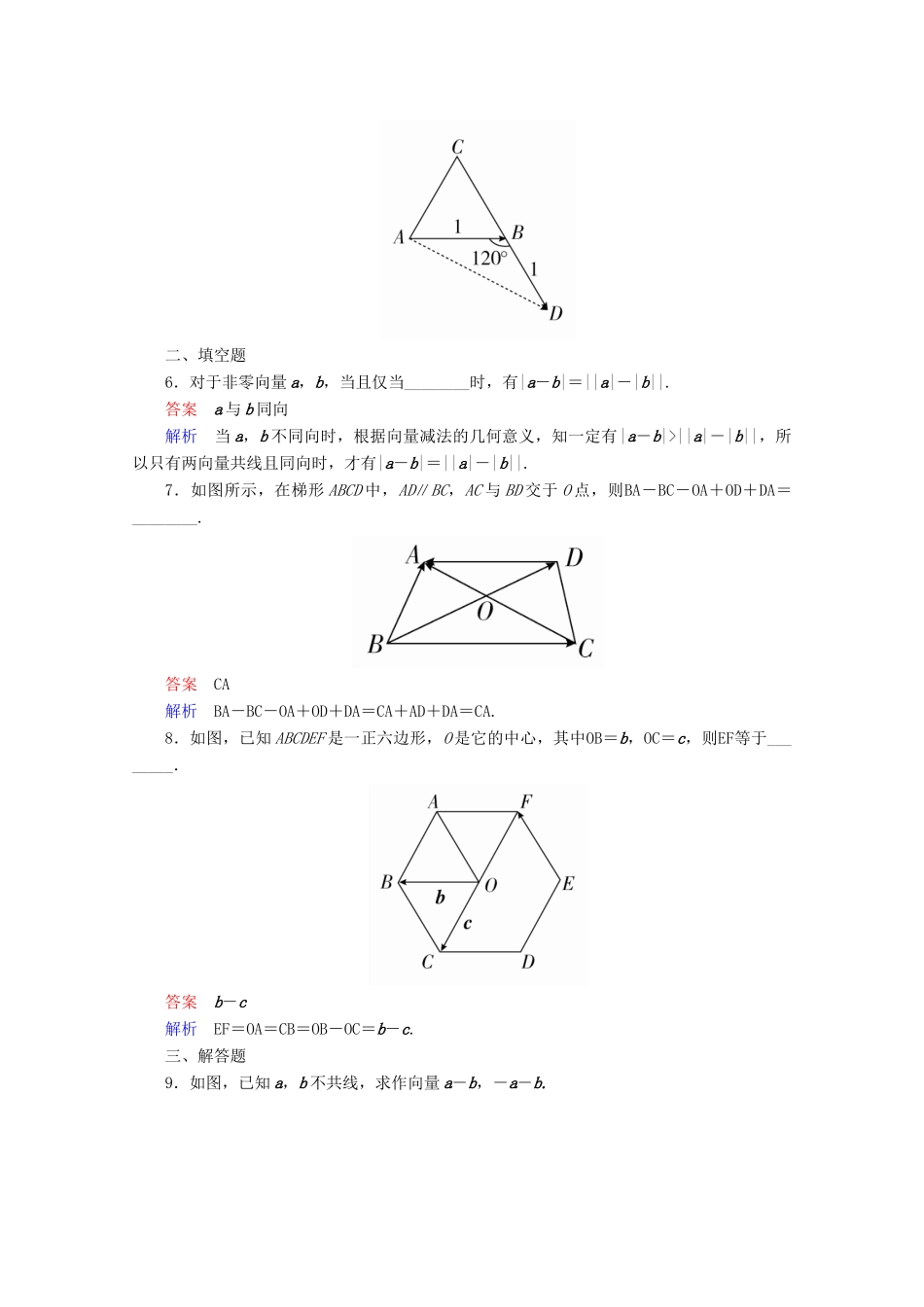
2.2.2向量减法运算及其几何意义A级:基础巩固练一、选择题1.下列运算中正确的是()A.OA-OB=ABB.AB-CD=DBC.OA-OB=BAD.AB-AB=0答案C解析根据向量减法的几何意义,知OA-OB=BA,所以C正确,A错误;B显然错误;对于D,AB-AB应该等于0,而不是0.2.下列说法错误的是()A.若OD+OE=OM,则OM-OE=ODB.若OD+OE=OM,则OM+DO=OEC.若OD+OE=OM,则OD-EO=OMD.若OD+OE=OM,则DO+EO=OM答案D解析由向量的减法就是向量加法的逆运算可知,A,B,C都正确.由相反向量定量知,共OD+OE=OM,则DO+EO=-OD-OE=-(OD+OE)=-OM,故D错误.3.有下列不等式或等式:①|a|-|b|<|a+b|<|a|+|b|;②|a|-|b|=|a+b|=|a|+|b|;③|a|-|b|=|a+b|<|a|+|b|;④|a|-|b|<|a+b|=|a|+|b|.其中,一定不成立的个数是()A.0B.1C.2D.3答案A解析①当a与b不共线时成立;②当a=b=0,或b=0,a≠0时成立;③当a与b共线,方向相反,且|a|≥|b|时成立;④当a与b共线,且方向相同时成立.4.AC可以写成:①AO+OC;②AO-OC;③OA-OC;④OC-OA,其中正确的是()A.①②B.②③C.③④D.①④答案D解析由向量的加法及减法定义可知①④符合.5.边长为1的正三角形ABC中,|AB-BC|的值为()A.1B.2C.D.答案D解析如图所示,延长CB到点D,使BD=1,连接AD,则AB-BC=AB+CB=AB+BD=AD.在△ABD中,AB=BD=1,∠ABD=120°,易求AD=,∴|AB-BC|=.二、填空题6.对于非零向量a,b,当且仅当________时,有|a-b|=||a|-|b||.答案a与b同向解析当a,b不同向时,根据向量减法的几何意义,知一定有|a-b|>||a|-|b||,所以只有两向量共线且同向时,才有|a-b|=||a|-|b||.7.如图所示,在梯形ABCD中,AD∥BC,AC与BD交于O点,则BA-BC-OA+OD+DA=________.答案CA解析BA-BC-OA+OD+DA=CA+AD+DA=CA.8.如图,已知ABCDEF是一正六边形,O是它的中心,其中OB=b,OC=c,则EF等于________.答案b-c解析EF=OA=CB=OB-OC=b-c.三、解答题9.如图,已知a,b不共线,求作向量a-b,-a-b.解如图(1),在平面内任取一点O,作OA=a,OB=b,则BA=OA-OB=a-b.如图(2),在平面内任取一点O,作OA=-a,OB=b,则BA=OA-OB=-a-b.10.设O是△ABC内一点,且OA=a,OB=b,OC=c,若以线段OA,OB为邻边作平行四边形,第四个顶点为D,再以OC,OD为邻边作平行四边形,其第四个顶点为H.试用a,b,c表示DC,OH,BH.解由题意可知四边形OADB为平行四边形,∴OD=OA+OB=a+b,∴DC=OC-OD=c-(a+b)=c-a-b.又四边形ODHC为平行四边形,∴OH=OC+OD=c+a+b,∴BH=OH-OB=a+b+c-b=a+c.B级:能力提升练1.设平面向量a1,a2,a3满足a1-a2+a3=0,如果平面向量b1,b2,b3满足|bi|=2|ai|,且ai顺时针旋转30°后与bi同向,其中i=1,2,3,则b1-b2+b3=________.答案0解析将ai顺时针旋转30°后得ai′,则a1′-a2′+a3′=0.又∵bi与ai′同向,且|bi|=2|ai|,∴b1-b2+b3=0.2.已知△ABC是等腰直角三角形,∠ACB=90°,M是斜边AB的中点,CM=a,CA=b.求证:(1)|a-b|=|a|;(2)|a+(a-b)|=|b|.证明因为△ABC是等腰直角三角形,∠ACB=90°,所以CA=CB.又M是斜边AB的中点,所以CM=AM=BM.(1)因为CM-CA=AM,又|AM|=|CM|,所以|a-b|=|a|.(2)因为M是斜边AB的中点,所以AM=MB,所以a+(a-b)=CM+(CM-CA)=CM+AM=CM+MB=CB,因为|CA|=|CB|,所以|a+(a-b)|=|b|.