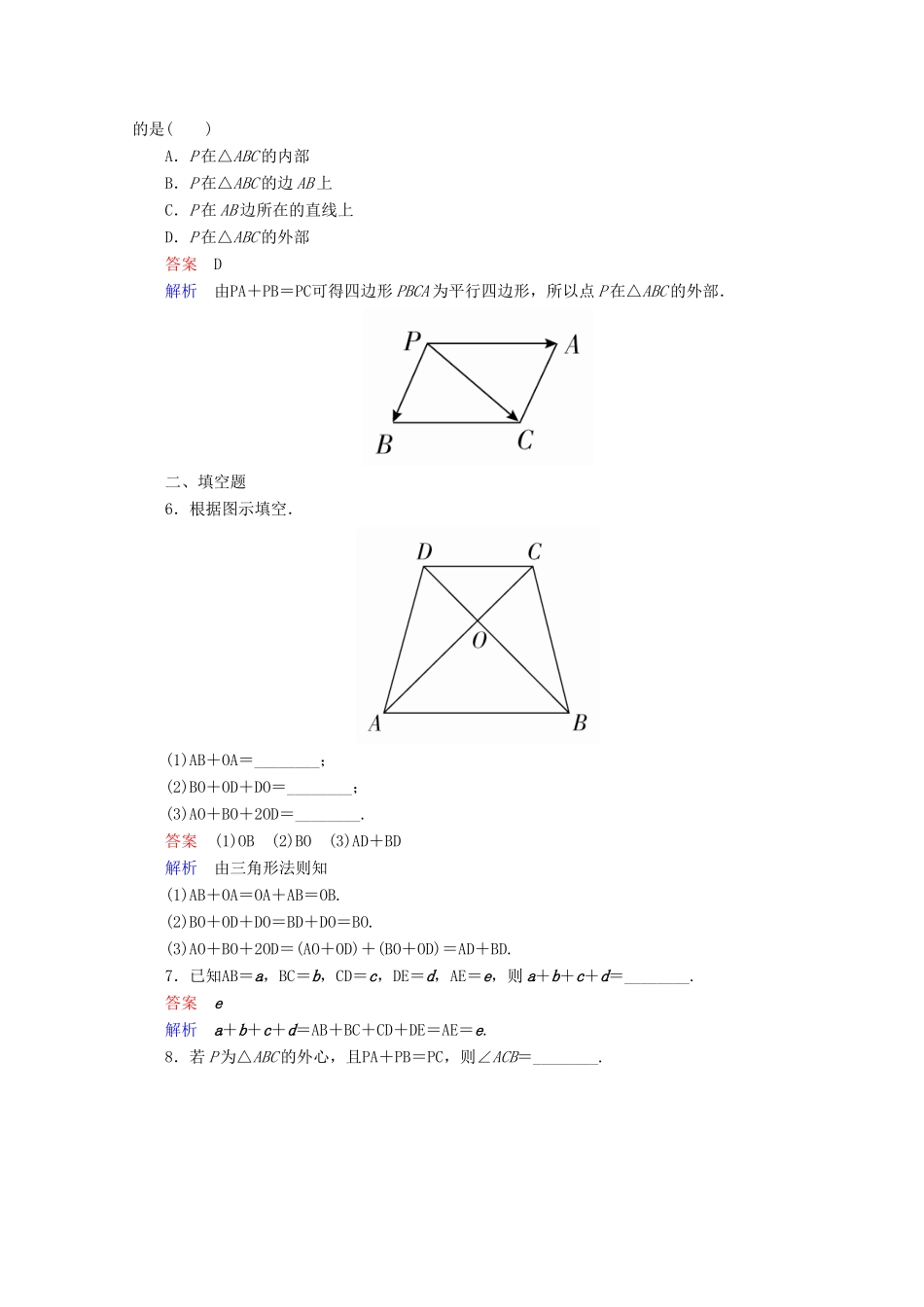
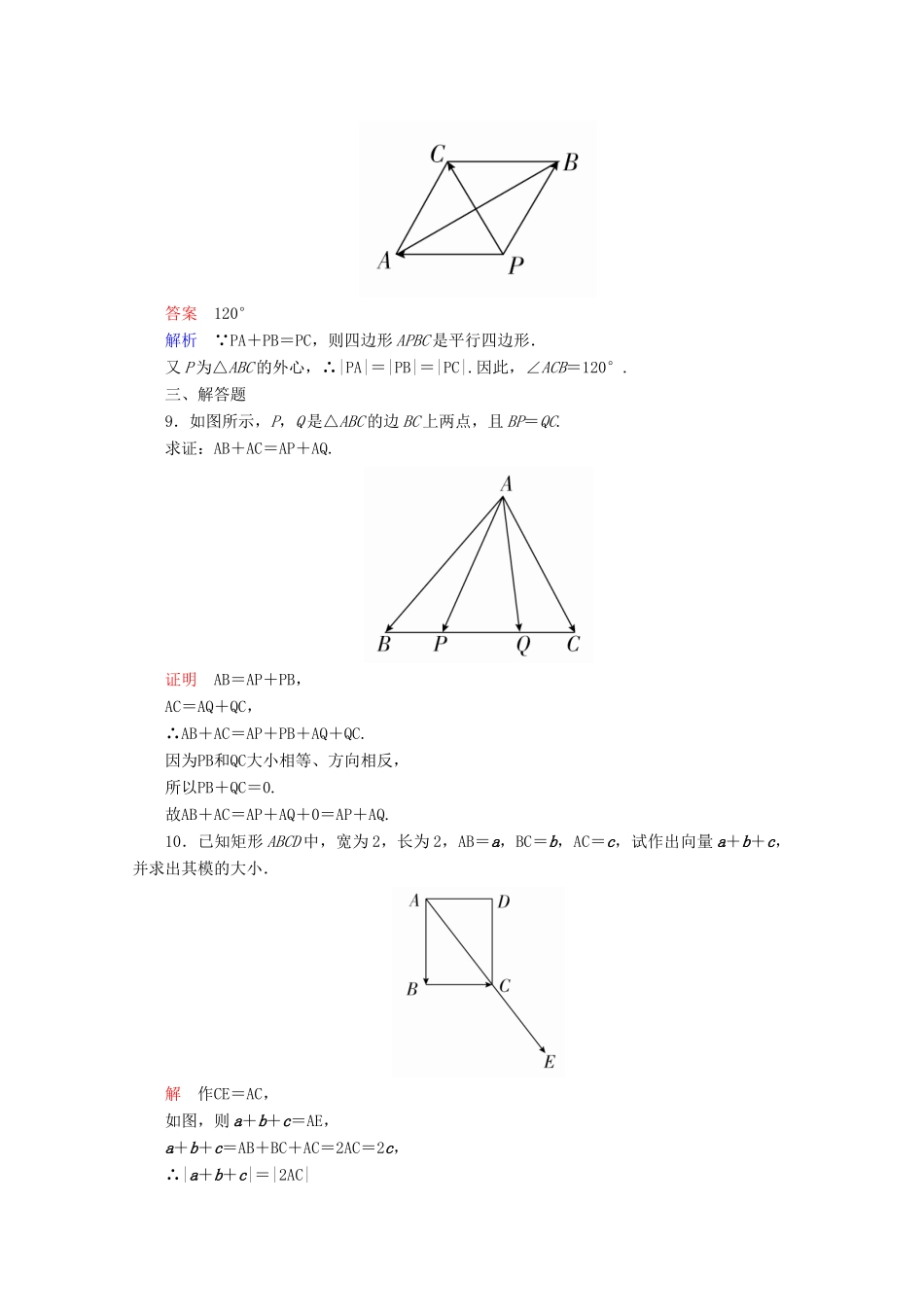
2.2.1向量加法运算及其几何意义A级:基础巩固练一、选择题1.在平行四边形ABCD中,下列式子:①AD=AB+BD;②AD=AC+CD;③AD+AB=AC;④AB+BC=AC;⑤AD=AB+BC+CD;⑥AD=DC+CA.其中不正确的个数是()A.1B.2C.4D.6答案A解析DC+CA=DA,故⑥不正确;其他都正确.2.设a=(AB+CD)+(BC+DA),b是任一非零向量,则在下列结论中,正确的是()①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;⑤|a+b|=|a|+|b|.A.①②B.①③C.①③⑤D.②④⑤答案C解析a=(AB+CD)+(BC+DA)=AB+BC+CD+DA=0,易知①③⑤正确.故选C.3.已知D,E,F分别是△ABC的边AB,BC,CA的中点,则下列等式中不正确的是()A.FD+DA=FAB.FD+DE+EF=0C.DE+DA=ECD.DA+DE=FD答案D解析由向量加法的平行四边形法则可知,DA+DE=DF≠FD.4.已知四边形ABCD是菱形,则下列等式中成立的是()A.AB+BC=CAB.AB+AC=BCC.AC+BA=ADD.AC+AD=DC答案C解析由四边形ABCD是菱形知CD=BA,则AC+BA=AC+CD=AD.故选C.5.已知△ABC的三个顶点A,B,C及平面内一点P满足PA+PB=PC,则下列结论中正确的是()A.P在△ABC的内部B.P在△ABC的边AB上C.P在AB边所在的直线上D.P在△ABC的外部答案D解析由PA+PB=PC可得四边形PBCA为平行四边形,所以点P在△ABC的外部.二、填空题6.根据图示填空.(1)AB+OA=________;(2)BO+OD+DO=________;(3)AO+BO+2OD=________.答案(1)OB(2)BO(3)AD+BD解析由三角形法则知(1)AB+OA=OA+AB=OB.(2)BO+OD+DO=BD+DO=BO.(3)AO+BO+2OD=(AO+OD)+(BO+OD)=AD+BD.7.已知AB=a,BC=b,CD=c,DE=d,AE=e,则a+b+c+d=________.答案e解析a+b+c+d=AB+BC+CD+DE=AE=e.8.若P为△ABC的外心,且PA+PB=PC,则∠ACB=________.答案120°解析∵PA+PB=PC,则四边形APBC是平行四边形.又P为△ABC的外心,∴|PA|=|PB|=|PC|.因此,∠ACB=120°.三、解答题9.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:AB+AC=AP+AQ.证明AB=AP+PB,AC=AQ+QC,∴AB+AC=AP+PB+AQ+QC.因为PB和QC大小相等、方向相反,所以PB+QC=0.故AB+AC=AP+AQ+0=AP+AQ.10.已知矩形ABCD中,宽为2,长为2,AB=a,BC=b,AC=c,试作出向量a+b+c,并求出其模的大小.解作CE=AC,如图,则a+b+c=AE,a+b+c=AB+BC+AC=2AC=2c,∴|a+b+c|=|2AC|=2=8.B级:能力提升练1.在四川5·12大地震后,一架救援直升飞机从A地沿北偏东60°方向飞行了40km到B地,再由B地沿正北方向飞行40km到达C地,求此时直升飞机与A地的相对位置.解如图所示,设AB,BC分别是直升飞机两次位移,则AC表示两次位移的合位移,即AC=AB+BC.在Rt△ABD中,|DB|=20km,|AD|=20km,在Rt△ACD中,|AC|==40km,∠CAD=60°,即此时直升飞机位于A地北偏东30°,且距离A地40km处.2.已知船在静水中的速度为20m/min,水流的速度为10m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.解作AB=v水,AD=v船,以AB,AD为邻边作▱ABCD,则AC=v实际,如图.由题意可知∠CAB=90°,在Rt△ABC中,|AB|=|v水|=10m/min,|BC|=|AD|=|v船|=20m/min,∴cos∠ABC===,∴∠ABC=60°,从而船与水流方向成120°角.故船行进的方向与水流的方向成120°角.