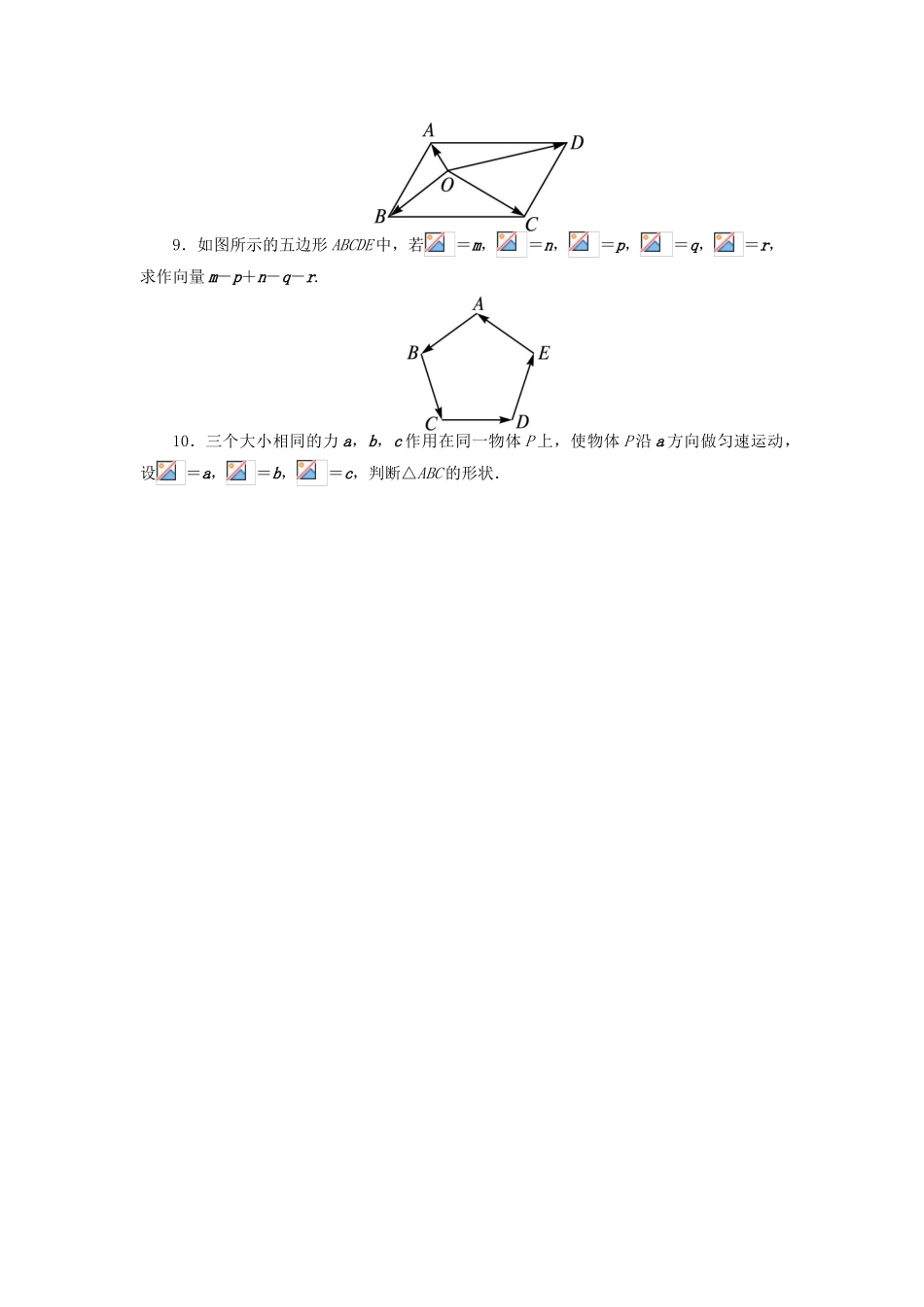
向量的减法1.如图所示,D,E,F分别是△ABC的边AB,BC,CA的中点,则-等于()A.B.C.D.2.(2012·山东潍坊期末)已知平行四边形ABCD,O是平行四边形ABCD所在平面外任意一点,=a,=b,=c,则向量等于()A.a+b+cB.a-b+cC.a+b-cD.a-b-c3.下列命题中,正确命题的个数为()①|a|+|b|=|a+b|a与b的方向相同;②|a|+|b|=|a-b|a与b的方向相反;③|a+b|=|a-b|a与b有相等的模;④|a|-|b|=|a-b|a与b的方向相同.A.0B.1C.2D.34.已知|a|=|b|=1,|a+b|=1,则|a-b|=()A.1B.C.D.25.平面上有三点A,B,C,设m=+,n=-,若m,n的长度恰好相等,则有()A.A,B,C三点必在同一直线上B.△ABC必为等腰三角形,且∠ABC为顶角C.△ABC必为直角三角形,且∠ABC=90°D.△ABC必为等腰直角三角形6.在边长为1的正方形ABCD中,设=a,=b,=c,则|a+b+c|=____________,|a+c-b|=____________,|c-a-b|=__________.7.已知△ABC为等腰直角三角形,且∠A=90°,有下列命题:①|AB+AC|=|AB-AC|;②|BC-BA|=|CB-CA|;③|AB-CB|=|AC-BC|;④|AB-AC|2=|BC-AC|2+|CB-AB|2.其中正确命题的序号为__________.8.如图,已知O为平行四边形ABCD内一点,=a,OB=b,OC=c,求OD.9.如图所示的五边形ABCDE中,若=m,=n,=p,=q,=r,求作向量m-p+n-q-r.10.三个大小相同的力a,b,c作用在同一物体P上,使物体P沿a方向做匀速运动,设=a,=b,=c,判断△ABC的形状.参考答案1.解析:由图可知=,则-=-=.又由三角形中位线定理,知=,故选D.答案:D2.解析:如图,有=+=+=+-=a+c-b.答案:B3.解析:当向量共线时,向量加法的平行四边形法则不适用,可考虑应用向量加法的三角形法则,其中①②是正确的;③由向量加减法的几何意义,知|a+b|=|a-b|等价于以a,b为邻边的平行四边形的对角线相等,此时a与b垂直,但a与b的模不一定相等,故③不正确;④不能判断|a|-|b|的符号,而|a-b|一定大于等于0,故④不正确.答案:C4.解析:如图所示,作平行四边形ABDC,根据向量加法的平行四边形法则可知,当|a|=|b|=1,|a+b|=1时,平行四边形ABDC为菱形.又|a+b|=1,所以△ABD为正三角形,所以∠ABD=60°.容易得出|a-b|=||=2||==2×=.答案:B5.解析:如图,作ABCD,则m=+=,n=-=-=.∵|m|=|n|,∴||=|DB|,∴ABCD为矩形.∴△ABC为直角三角形,∴∠ABC=90°.答案:C6.解析:|a+b+c|=2|c|=,|a+c-b|=|(c-b)+a|=2|a|=2,|c-a-b|=|c-(a+b)|=|c-c|=0.答案:207.解析:以AB,AC为邻边作平行四边形ABDC,由题意知其为正方形.∵|+|=||,|-|=||,||=||,∴①正确.②正确.∵|-|=|+|=||,|-|=|+|=||,又∵||=||,∴③正确.∵|-|2=||2,|-|2+|-|2=|+|2+|+|2=||2+||2=||2,∴④正确.答案:①②③④8.分析:所给图形是平行四边形,为了应用图形的性质,将向量,,,都转化到四条边上,由向量减法的三角形法则,得=-,=-.于是,根据与CD为相等向量的关系可得结论.解:因为=,=-,=-,所以-=-,=-+.所以=a-b+c.9.解:∵m-p+n-q-r=(m+n)-(p+q+r)=(+)-(++)=-=+,∴延长AC至点F,使||=||(如图),则=,∴=+,即向量即为所求作的向量m-p+n-q-r.10.解:由题意得|a|=|b|=|c|,由于合力作用后做匀速运动,故合力为0,即a+b+c=0.∴a+c=-b.如图所示,APCD为菱形,=a+c=-b.∴∠APC=120°,同理∠APB=∠BPC=120°.又∵|b|=|c|=|a|,∴易知△ABC为正三角形.