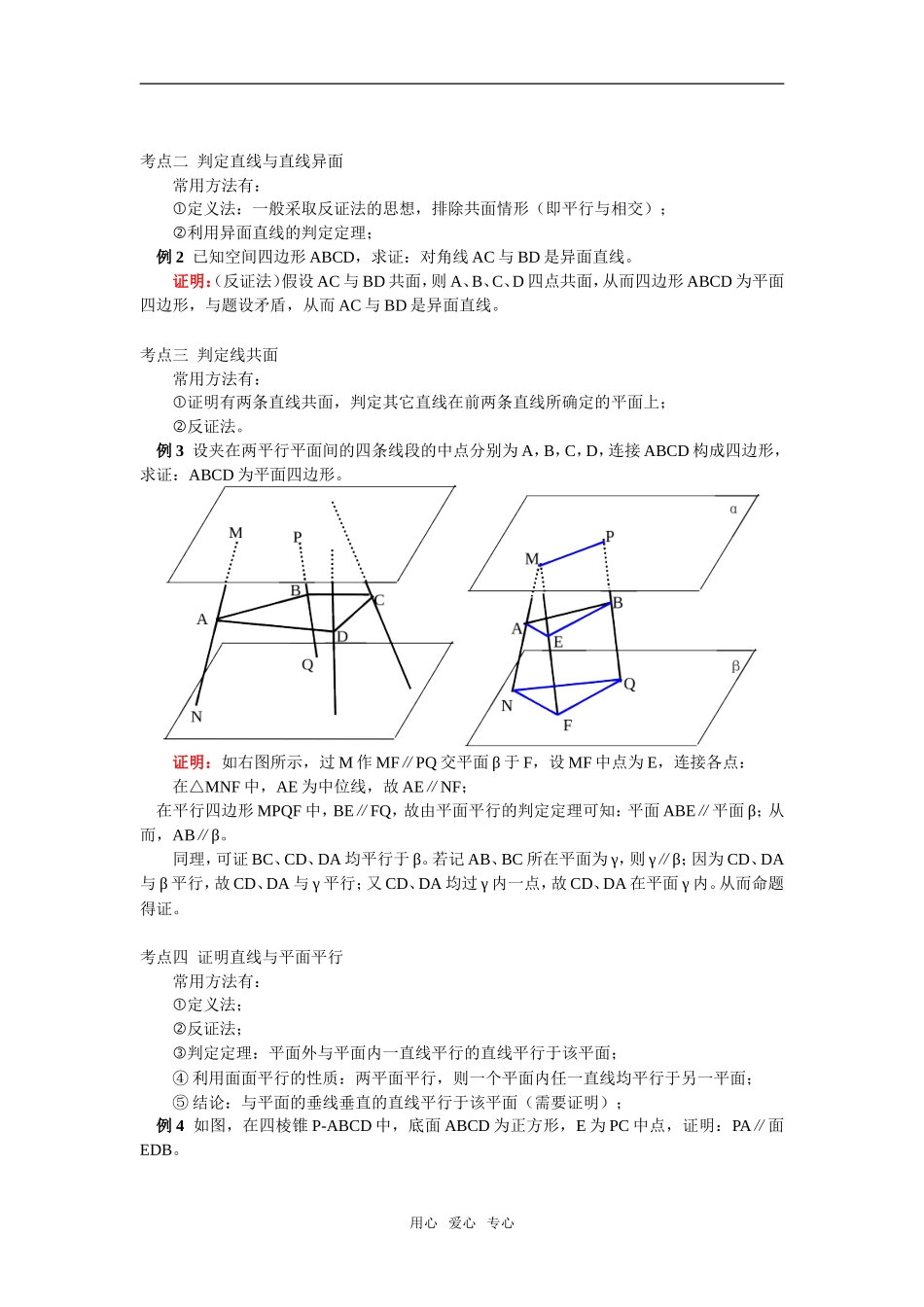
高一数学空间直线与直线、直线与平面的位置关系北师大版【本讲教育信息】一.教学内容:空间直线与直线、直线与平面的位置关系二.学习目标:1、了解空间直线与直线、直线与平面、平面与平面的位置关系;2、掌握空间位置关系的判定定理及其简单应用,了解定理的证明;3、掌握空间位置关系的性质定理及其简单应用,掌握定理的证明;4、通过一些典型题,掌握空间位置关系证明的常用方法;5、会求异面直线所成角及直线与平面所成角三.知识要点:1、空间直线与直线的位置关系(1)直线与直线平行(无公共点),记作a∥b;(2)直线与直线相交(有且仅有一个公共点),记作a∩b=A;(3)直线与直线异面(不同在任何一个平面内)说明:若进行两次分类,则可分为共面(包括平行、相交)与异面。它们的图形表示如下:2、直线和平面的位置关系(1)直线在平面内(无数个公共点),记作;(2)直线和平面相交(有且只有一个公共点),记作;(3)直线和平面平行(没有公共点),记作说明:若进行两次分类,则可分为直线在平面内和直线在平面外(包括相交、平行).它们的图形分别可表示为如下:aaAa3、线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行,即。4、线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行即:.5、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么用心爱心专心这条直线垂直于这个平面。即:。6、直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。即:。7、三垂线定理在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。三垂线定理的逆定理在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。8、异面直线所成角设a,b为异面直线,过空间任意一点作a,b的平行线,则平行线所成角即为异面直线所成角;直线与平面所成角平面的斜线与它在平面上的射影所成的角称为该斜线与平面所成角;若直线与平面平行,则所成角为0;若直线与平面垂直,则所成角为90°。四.考点解析与典型例题:考点一判定直线与直线平行常用方法有:定义法;平行平面的性质:两平行平面与第三个平面的交线互相平行;线面垂直的性质:垂直于同一个平面的两条直线互相平行;④如果一条直线与两个相交平面都平行,则该直线与相交平面的交线平行(此结论需证明);⑤三个平面两两相交有三条交线,如果有两条交线平行,则它们一定互相平行(此结论需要证明);⑥平行公理:平行于同一条直线的两条直线互相平行例1求证:垂直于同一个平面的两条直线互相平行。已知:a⊥α,b⊥α。求证:a∥b。证明:(同一法)过b上任一点M,作直线m∥a,因为a⊥α,由线面垂直的判定可知:m⊥α。从而过平面α外一点M有两条直线m,b均和α垂直,由线面垂直的性质“过一点作平面的垂线有且仅有一条”可知,m,b重合。因为m∥a,故b∥a.说明:严格地说,应用同一法进行命题证明的前提是先判断命题符合同一法则(即原命题和逆命题等价),但一般情况下判断命题是否符合同一法则比较困难,在几何中,同一法的一般做法是:要证A具有性质M,先作B具有性质M,然后说明A、B是同一个图形,从而A也具有性质M。用心爱心专心考点二判定直线与直线异面常用方法有:定义法:一般采取反证法的思想,排除共面情形(即平行与相交);利用异面直线的判定定理;例2已知空间四边形ABCD,求证:对角线AC与BD是异面直线。证明:(反证法)假设AC与BD共面,则A、B、C、D四点共面,从而四边形ABCD为平面四边形,与题设矛盾,从而AC与BD是异面直线。考点三判定线共面常用方法有:证明有两条直线共面,判定其它直线在前两条直线所确定的平面上;反证法。例3设夹在两平行平面间的四条线段的中点分别为A,B,C,D,连接ABCD构成四边形,求证:ABCD为平面四边形。证明:如右图所示,过M作MF∥PQ交平面β于F,设MF中点为E,连接各点:在△MNF中,AE为中位线,故AE∥NF;在平行四边形MPQF中...