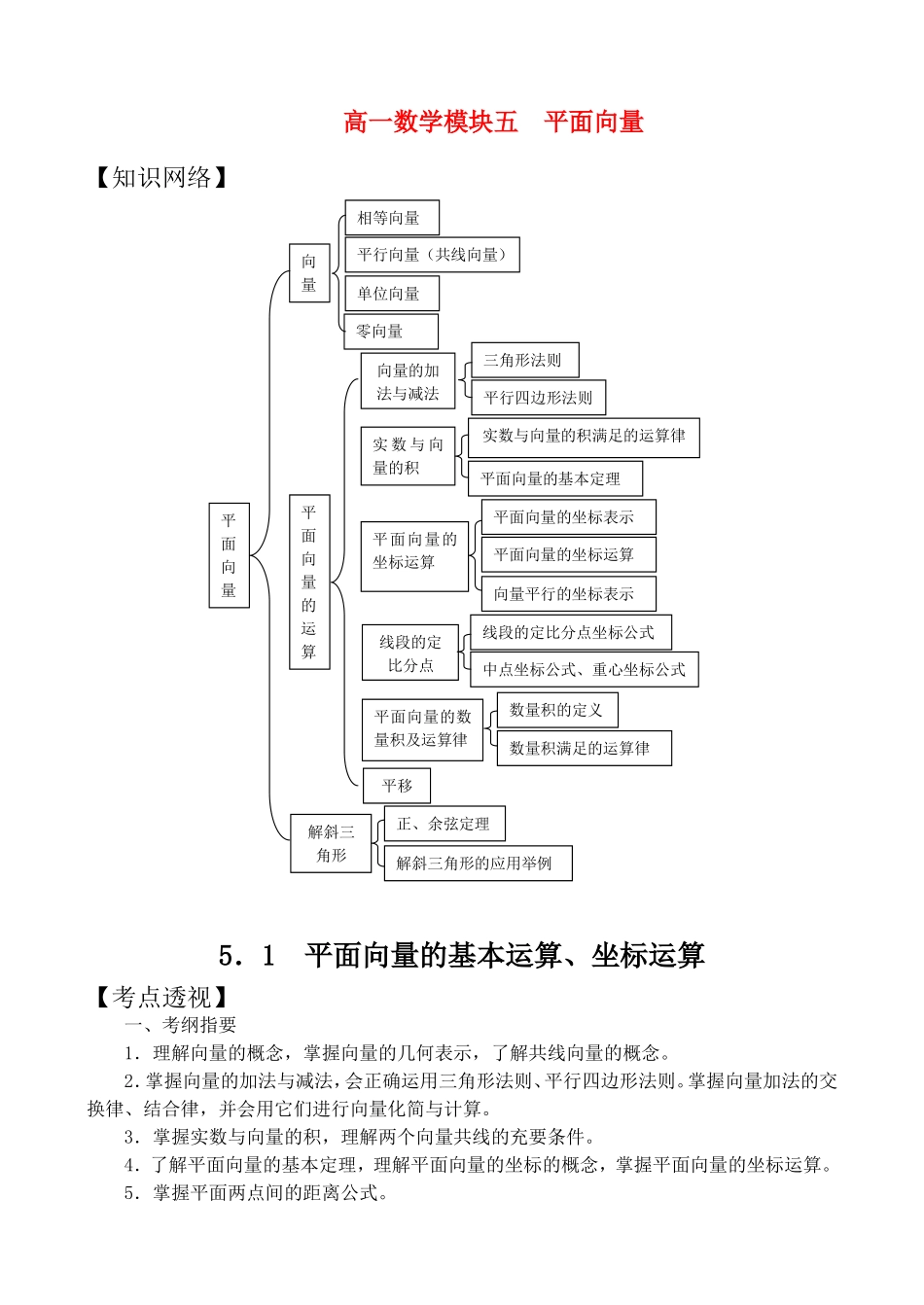
高一数学模块五平面向量【知识网络】平面向量的运算向量的加法与减法三角形法则平行四边形法则实数与向量的积满足的运算律实数与向量的积平面向量的基本定理平面向量的坐标表示平面向量的坐标运算平面向量的坐标运算向量平行的坐标表示线段的定比分点坐标公式线段的定比分点中点坐标公式、重心坐标公式平移平面向量的数量积及运算律数量积的定义数量积满足的运算律平面向量正、余弦定理解斜三角形解斜三角形的应用举例相等向量向量平行向量(共线向量)单位向量零向量5.1平面向量的基本运算、坐标运算【考点透视】一、考纲指要1.理解向量的概念,掌握向量的几何表示,了解共线向量的概念。2.掌握向量的加法与减法,会正确运用三角形法则、平行四边形法则。掌握向量加法的交换律、结合律,并会用它们进行向量化简与计算。3.掌握实数与向量的积,理解两个向量共线的充要条件。4.了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。5.掌握平面两点间的距离公式。二、命题落点1.考查向量的概念,向量加、减法几何运算及坐标运算。几何运算中要注意理解三角形法则,平行四边形法则;当向量运算转化成基底向量的代数式运算时,其运算过程可仿照多项式的加减运算进行。如例1和例2.2.向量的线性运算是向量运算中的基本内容,也是考查中的重点内容,尤其是对向量共线的充要条件,及平面向量基本定理的考查。如例2、例3.3.两个向量共线,或者三点共线问题。A、B、C三点共线的充要条件:存在实数λ,使得=λ。如例2和例4.4.在许多解析几何、平面几何问题中,用向量来解决显得格外简捷,作为一种工具,要达到得心应手、随心所欲的程度,关键应夯实基础。解析几何解答题和向量综合呈现了新高考的崭新亮点,体现了向量知识的工具性和广泛的应用性,是高考命题的主流方向。如例5.【典例精析】例1:(2003·全国)O是平面上的一定点,A、B、C是平面上不共线的3个点,动点P满足,则P点的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心解析:本题考查向量的概念,向量加、减法运算的几何意义.已知式可化为,令,则得,∴P的轨迹是∠BAC的平分线,所以P点通过△ABC的内心.答案:B例2:(2002·天津文)平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足,其中α、β∈R,且α+β=1,则点C的轨迹方程为()A.3x+2y-11=0B.(x-1)2+(y-2)2=5C.2x-y=0D.x+2y-5=0解析:本题主要考查向量法和坐标法的相互关系及转换方法.设=(x,y),=(3,1),=(-1,3),α=(3α,α),β=(-β,3β).又α+β=(3α-β,α+3β),∴(x,y)=(3α-β,α+3β),∴,又α+β=1,因此可得x+2y=5.答案:D.例3:(1997·全国)过原点O的直线与函数图象交于A、B两点,过A、B分别作轴的垂线交函数的图像于C、D两点,求证:O、C、D三点共线.解析:利用向量共线证明.设、. 与共线,∴,又由题意知,,即,. ,∴、共线,∴O、C、D三点共线.利用向量证明三点共线,或者证明两条线段平行须分两步完成:①证明两个向量平行;②说明两个向量有公共点.【常见误区】1.正确处理几个问题:(1)正确区分向量\s\up7(→)与实数a、\s\up7(→)与0.(2)正确区分向量运算与实数运算.2.向量运算,要注意向量的方向不能搞错。如三角形中两边对应向量已知,求第三边所对应的向量时,利用向量加减法的三角形法则实施求解,一定要注意向量的方向.3.平面向量的运算表现在两个方面,向量的几何运算与向量的坐标运算,可以从不同角度去求解(证)同一个问题.只不过两套工具各有适用范围,即便两套工具都适用,也可能繁简不一,应选用哪一种运算要根据实际情况来定。在坐标运算中,合理地选择坐标系有利于优化解题过程.【基础演练】1.(2006·全国)已知向量满足,且,则与的夹角为()A.B.C.D.2.(2005·山东)已知向量,且,,则一定共线的三点是()A.A、B、DB.A、B、CC.B、C、DD.A、C、D3.(2005·全国)点在平面上作匀速直线运动,速度向量(即点的运动方向与相同,且每秒移动的距离为个单位).设开始时点的坐标为...