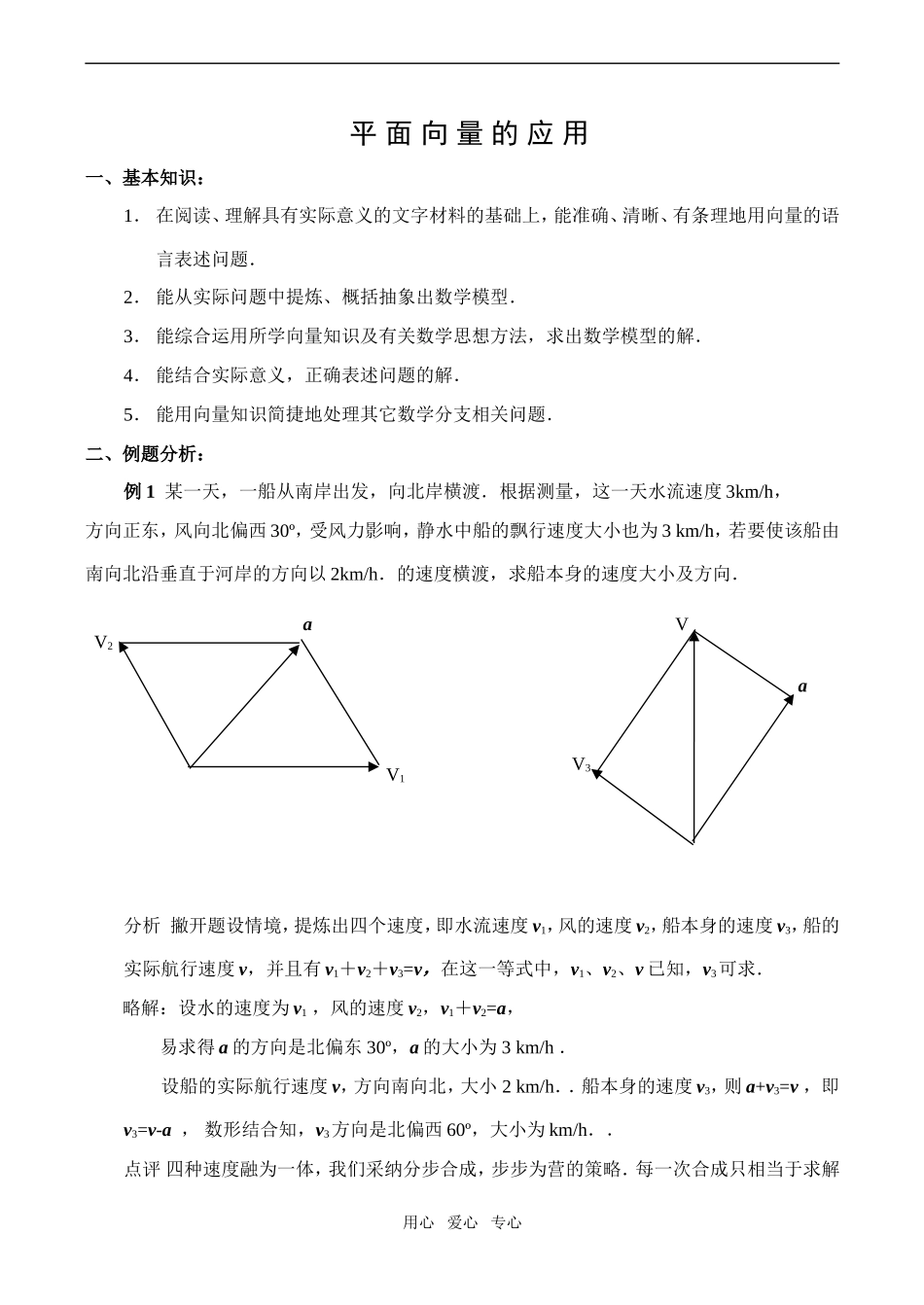
平面向量的应用一、基本知识:1.在阅读、理解具有实际意义的文字材料的基础上,能准确、清晰、有条理地用向量的语言表述问题.2.能从实际问题中提炼、概括抽象出数学模型.3.能综合运用所学向量知识及有关数学思想方法,求出数学模型的解.4.能结合实际意义,正确表述问题的解.5.能用向量知识简捷地处理其它数学分支相关问题.二、例题分析:例1某一天,一船从南岸出发,向北岸横渡.根据测量,这一天水流速度3km/h,方向正东,风向北偏西30º,受风力影响,静水中船的飘行速度大小也为3km/h,若要使该船由南向北沿垂直于河岸的方向以2km/h.的速度横渡,求船本身的速度大小及方向.分析撇开题设情境,提炼出四个速度,即水流速度v1,风的速度v2,船本身的速度v3,船的实际航行速度v,并且有v1+v2+v3=v,在这一等式中,v1、v2、v已知,v3可求.略解:设水的速度为v1,风的速度v2,v1+v2=a,易求得a的方向是北偏东30º,a的大小为3km/h.设船的实际航行速度v,方向南向北,大小2km/h..船本身的速度v3,则a+v3=v,即v3=v-a,数形结合知,v3方向是北偏西60º,大小为km/h..点评四种速度融为一体,我们采纳分步合成,步步为营的策略.每一次合成只相当于求解用心爱心专心aVV3V1V2a了一个简单题.例2已知O为ΔABC所在平面内一点,满足|OA|2+|BC|2=|CA|2+|OB|2=|OC|2+|AB|2.试证明O是ΔABC的垂心.分析已知等式是关于线段长度平方和的等式,OA与BC、OB与CA、OC与AB都不是同一个直角三角形中的线段,用纯平面几何知识证明相当困难.但线段长度平方和即向量模的平方,要证O是ΔABC的垂心,只需证得OA⊥BC,OB⊥CA,联想向量的数量积,只需证OA·BC=OB·CA=0.|OA|2+|BC|2=|CA|2+|OB|2,得a2+(c-b)2=b2+(a-c)2,c·b=a·c,即(b-a)·c=0.OC·AB=0,故AB⊥OC.同理CA⊥OB,BC⊥OA.故O是ΔABC的垂心.点评向量知识的应用领域很宽泛,中学数学所涉及的平几、方程、数列、不等式等等,都可以与向量综合,求解这类问题的关键在于揭去伪装,合理转化.例3.如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1∶m2=OB∶OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:(1)∠AOB为定值;(2)>2.用心爱心专心BOmm2Am1分析依据题意,我们可以作出物体的受力图,引用平衡条件可列出方程组,在方程组的变形中,探索∠AOB的大小,在求出∠AOB后,再向第2问结论努力.解(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.如图,设∠BAO=α,∠ABO=β,根据平行四边形法则,得F2cosβ+F1cos(π-α)=0,F2sinβ+F1sin(π-α)+F=0.即m2cosβ-m1cosα=0,①m2sinβ+m1sinα=m.②在ΔAOB中,由正弦定理,得OB∶OA=sinα∶sinβ,将m1∶m2=sinα∶sinβ代入①,得sinβcosβ=sinαcosα,即sin2β=sin2α. m1≠m2,∴OA≠OB.∴α≠β,2α+2β=180º.∴α+β=90º,即∠AOB=90º.(2)由α+β=90º,得cosβcosα=sinβsinα.将①②平方相加,得m2=m12+m22.由m2-2m1m2=m12+m22-2m1m2=(m1-m2)2>0,得m2>2m1m2.∴>2.点评向量在物理中的应用最常见的是力学问题,物体处于平衡状态即所受各力的合力为0,亦即向量之和为零向量,运用三角形法则、平行四边形法则及解斜三角形的基础知识可望得到问题的解.本题所列方程组,是根据物体水平方向、竖直方向所受各力的合力分别为0得到.用心爱心专心F2F1FBA三、训练反馈:1.如果一架向东飞行200km,再向南飞行300km,记飞机飞行的路程为s,位移为a,则(A)A.s>|a|B.s<|a|C.s=|a|D.s与|a|不能比大小2.一条河宽为d,水流速度为v2,一船从岸边A处出发,垂直河岸线航行到河的正对岸B处,船在静水中的速度为v1,则船在航行过程中,船的实际航行速度大小为(C)A.|v1|B.C.D.|v1|-|v2|3.一艘船以4km/h的速度,沿着与水流方向成120º的方向航行,已知河水流速为2km/h,该船若航行6km...