高一数学对数函数苏教版VIP免费

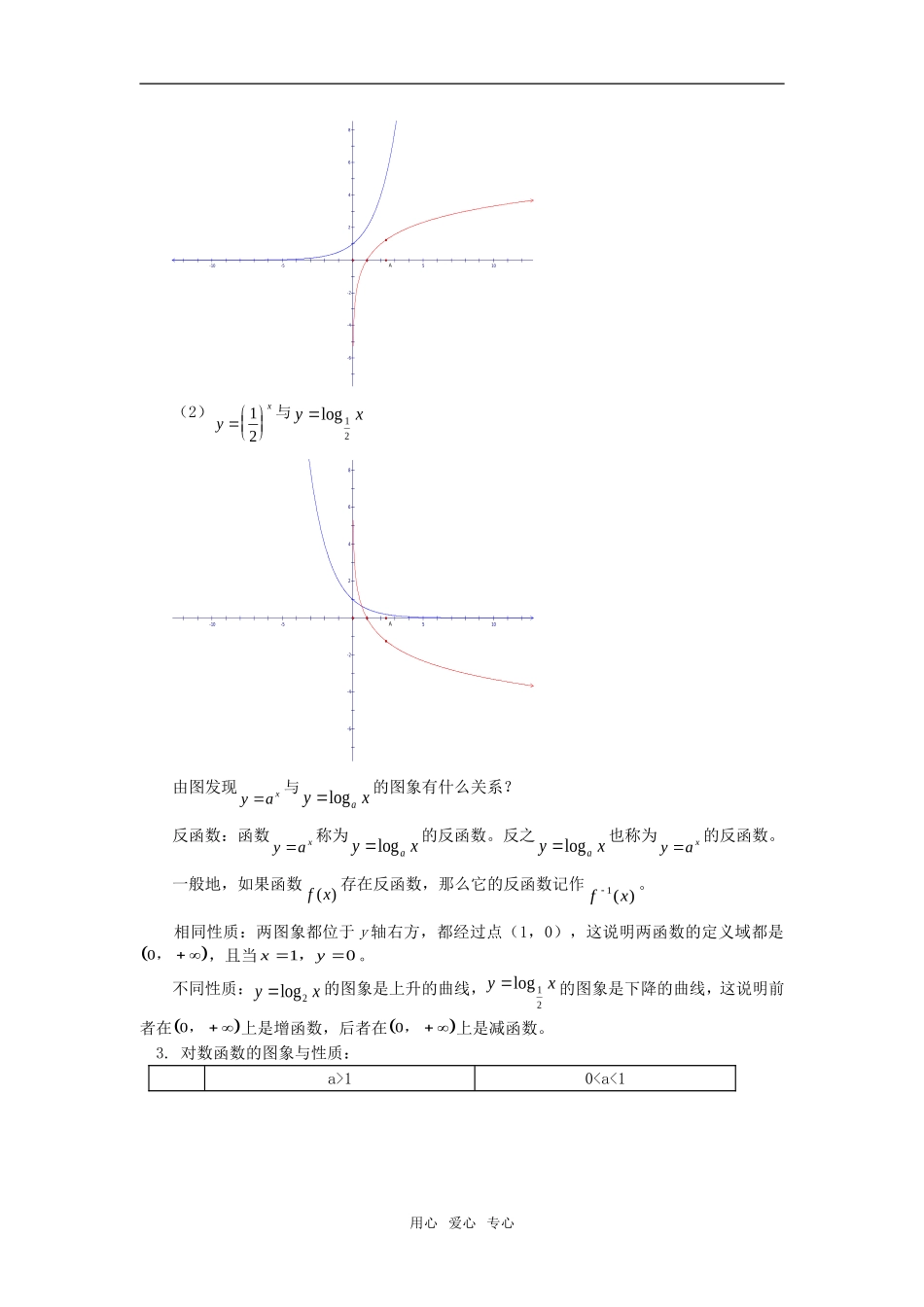
高一数学对数函数苏教版【本讲教育信息】一.教学内容：对数函数【教学目标】1.理解对数的概念及其运算性质，会熟练地进行指数式与对数式的互化，能灵活准确地运用对数的运算性质进行对数、对数式的化简与计算；了解对数恒等式，知道用换底公式能将一般对数化成自然对数或常用对数，会用换底公式进行一些简单的化简与证明。2.通过具体的实例，直观了解对数函数的模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型。3.知道指数函数yaaax()01，与对数函数yxaaalog01，互为反函数；能运用对数函数的性质比较两个对数式值的大小；能研究一些与对数函数有关的复合函数的定义域、值域、单调性等。4.感受化归与转化、数形结合的思想。【教学过程】（一）对数的概念庄子：一尺之棰，日取其半，万世不竭。（1）取5次，还有多长？取多少次，还有0.125尺？（2）某种放射性物质不断变化为其他物质，每经过一年，这种物质的剩留量是原来的84%，试问经过多少年，这种物质的剩留量是原来的一半？抽象出：（1）125?，120125xx.?（2）08412.?xx1.定义：一般地，如果aaa()01，的b次幂等于N，就是aNb，那么数b叫做以a为底N的对数，记作log()aNblogarithm，a叫做对数的底数（baseoflogarithm），N叫做真数（propernumber）。说明：（1）aNb与logaNb等价（2）a，N，b的取值范围各是：①a0且a1；②N＞0；③bR2.几个常用的对数等式：loglogloglogaaanNaanaNa101，，，3.常用对数与自然对数：常用对数：我们通常将以10为底的对数叫做常用对数。为了简便，N的常用对数log10N简记作lgN。用心爱心专心例如：log105简记作lg5；log.1035简记作lg.35。自然对数：在科学技术中常常使用以无理数e2.71828……为底的对数，以e为底的对数叫自然对数，为了简便，N的自然对数logeN简记作lnN。例如：loge3简记作ln3；10loge简记作ln10。（二）对数的运算法则1.运算法则的内容：loglogloglogloglogloglogaaaaaaanaMNMNaaMNMNMNaaMNMnMaaMnR01000100010，，，，，，·，，，（三）换底公式logloglogaccNNaNaacc00101，，且，且说明：换底公式的意义是把一个对数式的底数改变，可将不同底问题化为同底，便于使用运算法则。如换底公式可以解决如下问题：（1）loglogabba·1（2）loglogamanbmnbaba·，且001（四）对数函数我们研究指数函数时，曾经讨论过细胞分裂问题，某种细胞分裂时，得到的细胞的个数y是分裂次数x的函数，这个函数可以用指数函数yx2表示。现在，我们来研究相反的问题，如果要求这种细胞经过多少次分裂，大约可以得到1万个，10万个……细胞，那么，分裂次数x就是要得到的细胞个数y的函数。根据对数的定义，这个函数可以写成对数的形式就是xylog2，把y看作自变量，x就是y的函数，这样就得到一个新函数。1.定义：函数yxaaalog01，且叫做对数函数；它的定义域是0，。2.对数函数的图象与性质（1）yx2与yxlog2用心爱心专心8642-2-4-6-10-5510A（2）yx12与yxlog128642-2-4-6-10-5510A由图发现yax与yxalog的图象有什么关系？反函数：函数yax称为yxalog的反函数。反之yxalog也称为yax的反函数。一般地，如果函数fx()存在反函数，那么它的反函数记作fx1()。相同性质：两图象都位于y轴右方，都经过点（1，0），这说明两函数的定义域都是0，，且当xy10，。不同性质：yxlog2的图象是上升的曲线，yxlog12的图象是下降的曲线，这说明前者在0，上是增函数，后者在0，上是减函数。3.对数函数的图象与性质：a>10