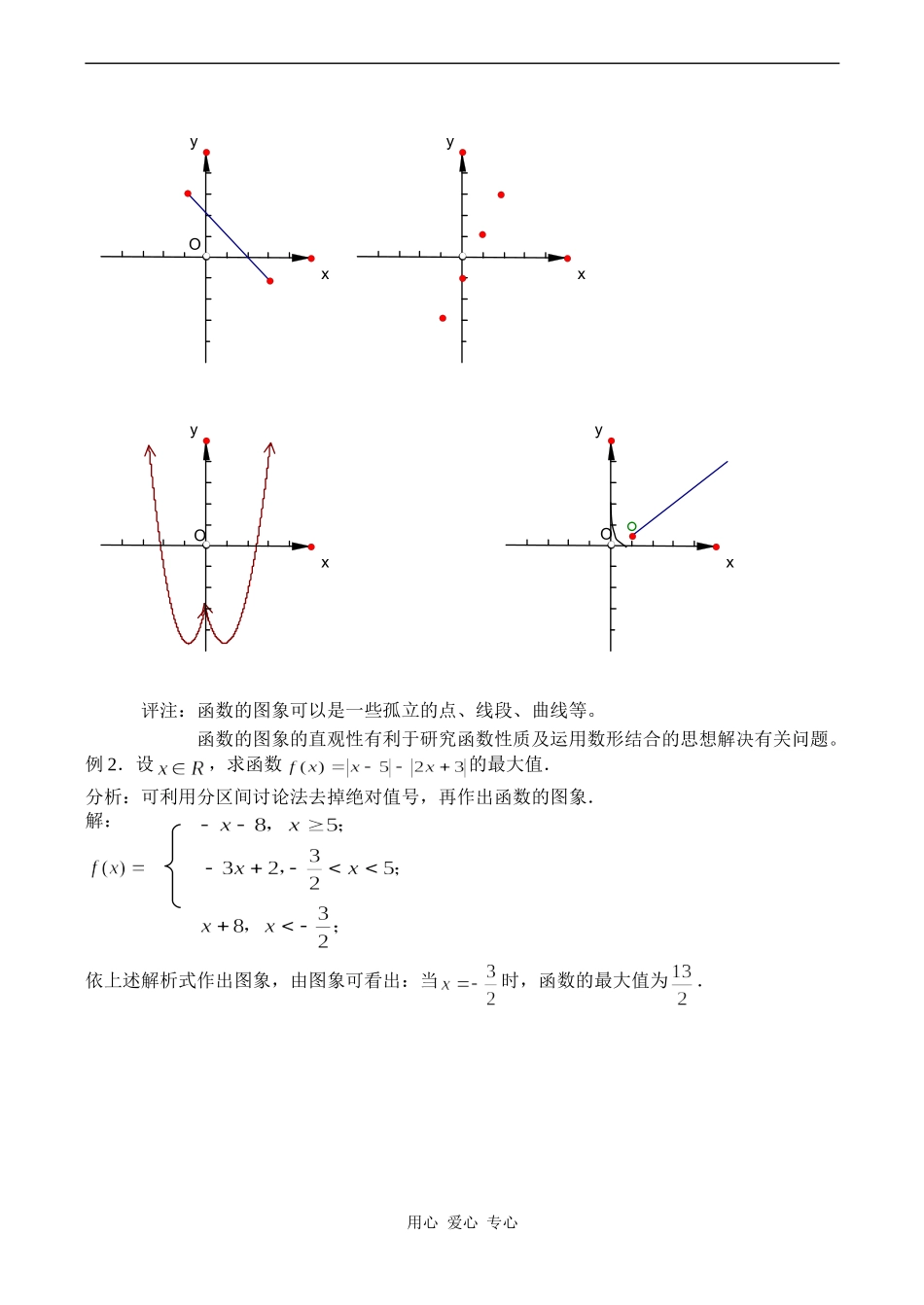
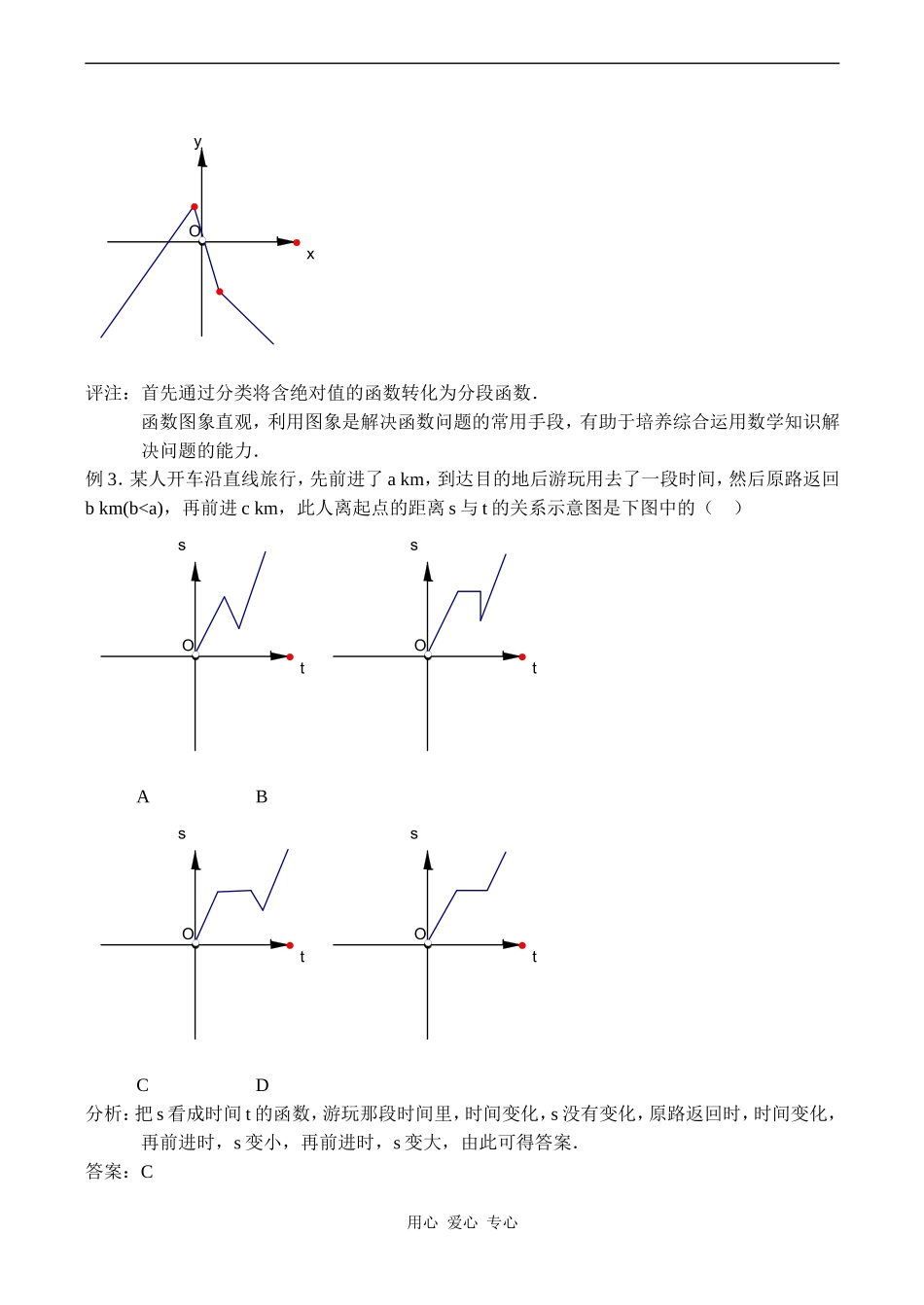
函数的概念和图象教学目标:1.会用描点法和基本初等函数的图象作出函数的图象,掌握函数图象的简单应用.2.通过函数的作图过程体会函数思想.3.培养观察问题、提出问题、分析问题、解决问题的探究能力,运用数形结合思想的能力,培养应用数学的意识,激发学习数学的兴趣,提高数学素质.学习指导:本课的重点是作出函数的图象及函数图象的简单运用.难点是数形结合思想及应用数学的意识的渗透.学习中应注意以下两点:(1)根据函数的解析式画出函数的图象时,要注意定义域对函数图象的制约;(2)注意函数本身的特点,如二次函数图象的顶点,对称性等,有利于比较准确地作出函数的图象;(3)函数的图象既是下面研究函数性质的重要工具,又是数形结合思想的基础,因此必须予以重视.另外,在对实际问题的探究中,体会函数图象的直观性、数形结合的思想及函数在生产生活中的应用.有助于正确了解函数概念和性质,便于发现问题、启发思考,有助于培养综合运用数学知识解决问题的能力.例题精析:例1.作出下列函数的图象:(1);(2);(3);(4).分析:函数图象常用作图方法有两种:(1)描点作图法;(2)利用基本初等函数的图象作出所求函数的图象解:(1)这个函数的图象是一条线段.(2)这个函数的图象有一些点组成,这些点都在直线上,这些点称为整点.(3)图象由关于y轴对称的两部分组成;(4)图象由两部分组成:当时,为双曲线的一段;当时,为直线的一段.用心爱心专心OxyxyOxyOxy评注:函数的图象可以是一些孤立的点、线段、曲线等。函数的图象的直观性有利于研究函数性质及运用数形结合的思想解决有关问题。例2.设,求函数的最大值.分析:可利用分区间讨论法去掉绝对值号,再作出函数的图象.解:依上述解析式作出图象,由图象可看出:当时,函数的最大值为.用心爱心专心yOx评注:首先通过分类将含绝对值的函数转化为分段函数.函数图象直观,利用图象是解决函数问题的常用手段,有助于培养综合运用数学知识解决问题的能力.例3.某人开车沿直线旅行,先前进了akm,到达目的地后游玩用去了一段时间,然后原路返回bkm(b