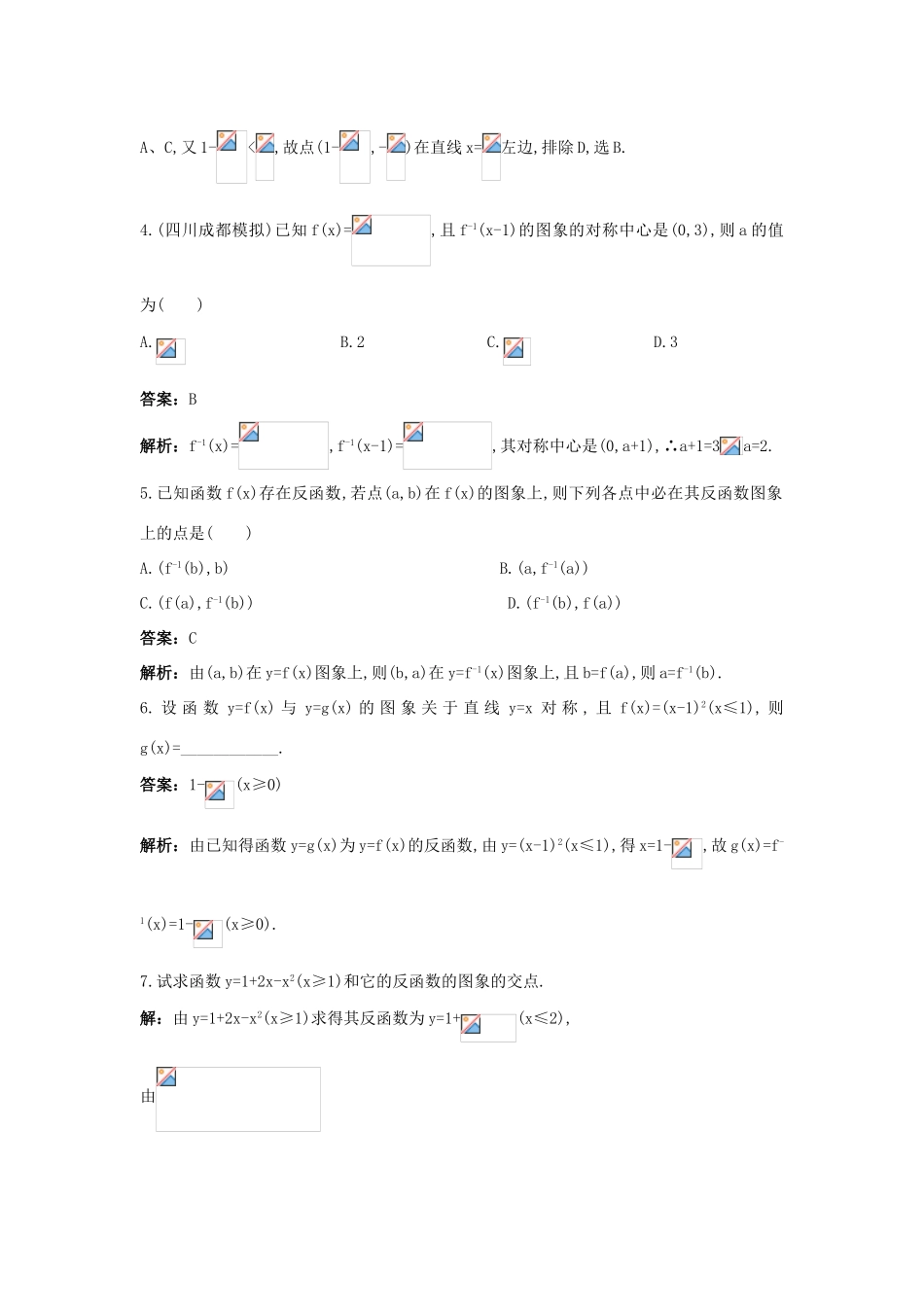
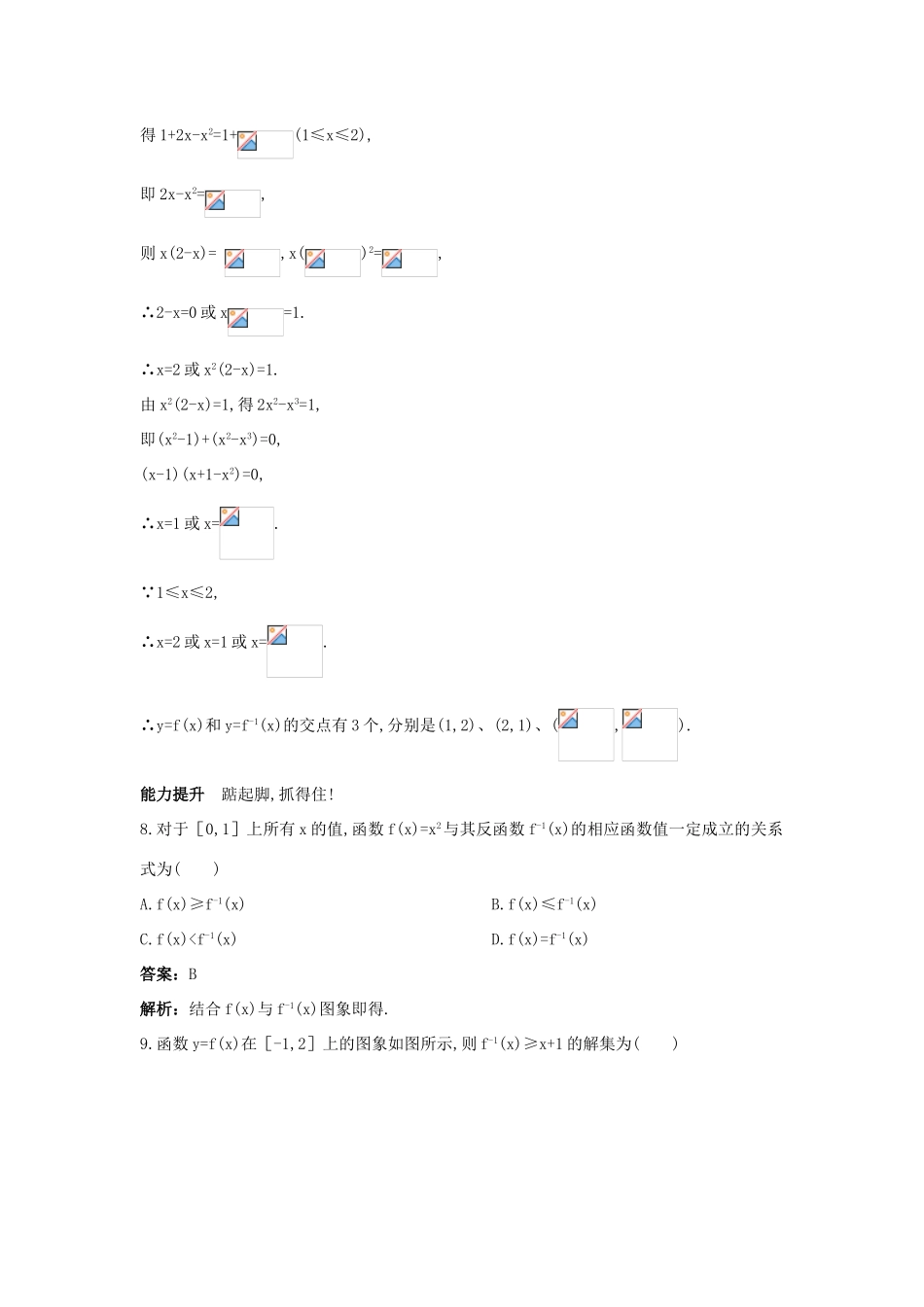
互为反函数的函数图象间的关系基础巩固站起来,拿得到!1.点(3,5)在函数y=ax+b的图象上,又在其反函数的图象上,则a、b的值分别为()A.a=-1,b=7B.a=-1,b=-8C.a=-1,b=8D.以上都不对答案:C解析:由已知得点(3,5)和点(5,3)在直线y=ax+b上,∴2.已知f(x)=的图象关于直线y=x对称,则a的取值是()A.-1B.1C.-2D.0答案:A解析:由y=,得x=,故f-1(x)=,因函数f(x)的图象关于直线y=x对称,则f(x)与其反函数f-1(x)为同一函数,易得a=-1.3.如图,设函数y=1-(-1≤x≤0),则函数y=f-1(x)的图象是图中的()答案:B解析:易知点(-,1-)在原函数图象上,故(1-,-)在其反函数图象上,首先排除A、C,又1-<,故点(1-,-)在直线x=左边,排除D,选B.4.(四川成都模拟)已知f(x)=,且f-1(x-1)的图象的对称中心是(0,3),则a的值为()A.B.2C.D.3答案:B解析:f-1(x)=,f-1(x-1)=,其对称中心是(0,a+1),∴a+1=3a=2.5.已知函数f(x)存在反函数,若点(a,b)在f(x)的图象上,则下列各点中必在其反函数图象上的点是()A.(f-1(b),b)B.(a,f-1(a))C.(f(a),f-1(b))D.(f-1(b),f(a))答案:C解析:由(a,b)在y=f(x)图象上,则(b,a)在y=f-1(x)图象上,且b=f(a),则a=f-1(b).6.设函数y=f(x)与y=g(x)的图象关于直线y=x对称,且f(x)=(x-1)2(x≤1),则g(x)=____________.答案:1-(x≥0)解析:由已知得函数y=g(x)为y=f(x)的反函数,由y=(x-1)2(x≤1),得x=1-,故g(x)=f-1(x)=1-(x≥0).7.试求函数y=1+2x-x2(x≥1)和它的反函数的图象的交点.解:由y=1+2x-x2(x≥1)求得其反函数为y=1+(x≤2),由得1+2x-x2=1+(1≤x≤2),即2x-x2=,则x(2-x)=,x()2=,∴2-x=0或x=1.∴x=2或x2(2-x)=1.由x2(2-x)=1,得2x2-x3=1,即(x2-1)+(x2-x3)=0,(x-1)(x+1-x2)=0,∴x=1或x=.∵1≤x≤2,∴x=2或x=1或x=.∴y=f(x)和y=f-1(x)的交点有3个,分别是(1,2)、(2,1)、(,).能力提升踮起脚,抓得住!8.对于[0,1]上所有x的值,函数f(x)=x2与其反函数f-1(x)的相应函数值一定成立的关系式为()A.f(x)≥f-1(x)B.f(x)≤f-1(x)C.f(x)-1)的图象与其反函数的图象的交点坐标为_________________.答案:(0,0),(1,1)解析:由y=,得x=.由x>-1,得<1,即y<2.∴其反函数为f-1(x)=(x<2).由得∴12.已知函数f(x)=,(1)求反函数f-1(x);(2)研究f-1(x)的单调性;(3)在同一坐标系中,画出f(x)与f-1(x)的图象.解:(1)∵f(x)==y,∴x+5=y2,且y≥0.∴x=y2-5.则f(x)=的反函数为y=f-1(x)=x2-5(x≥0).(2)由二次函数的图象知当x≥0时,f-1(x)为增函数.(3)图象如图所示.13.已知函数f(x)=2x2-4x+1,x∈[-1,0].(1)求f-1(x);(2)作出y=f(x)和y=f-1(x)的图象,并判断其单调性;(3)解不等式:f-1(7x)x+1≥1.解得0,∴=,x=(y+)2.∴f-1(x)=(x+)2(x∈R).(2)解:y=f-1(x)与y=f(x)的图象关于y=x对称,故只需判断y=f(x)与y=x有无交点.由得x=.∴x(1-)=1.当0