2022年中考数学几何模型之单中点与双中点模型讲+练原卷版VIP免费

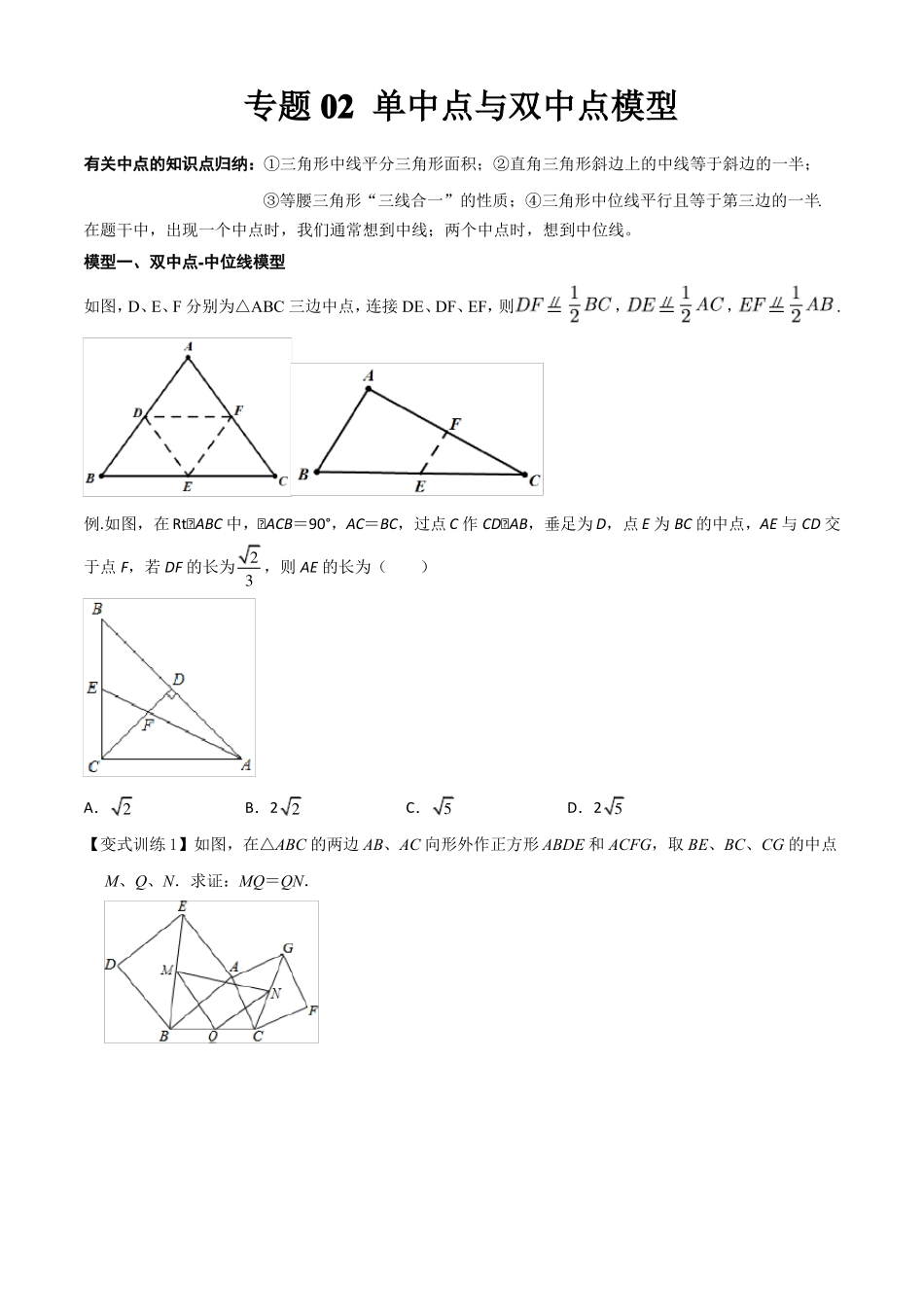
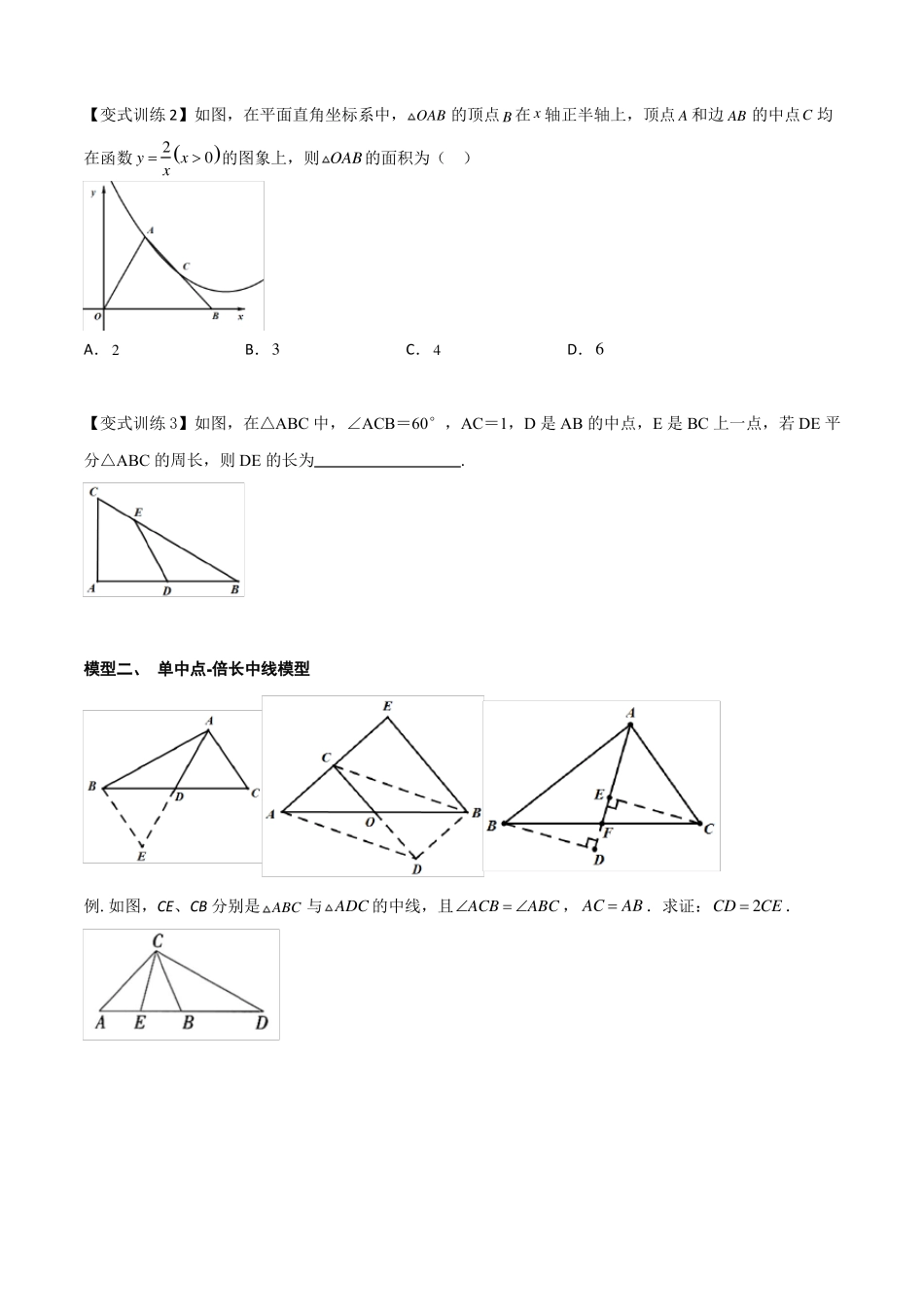
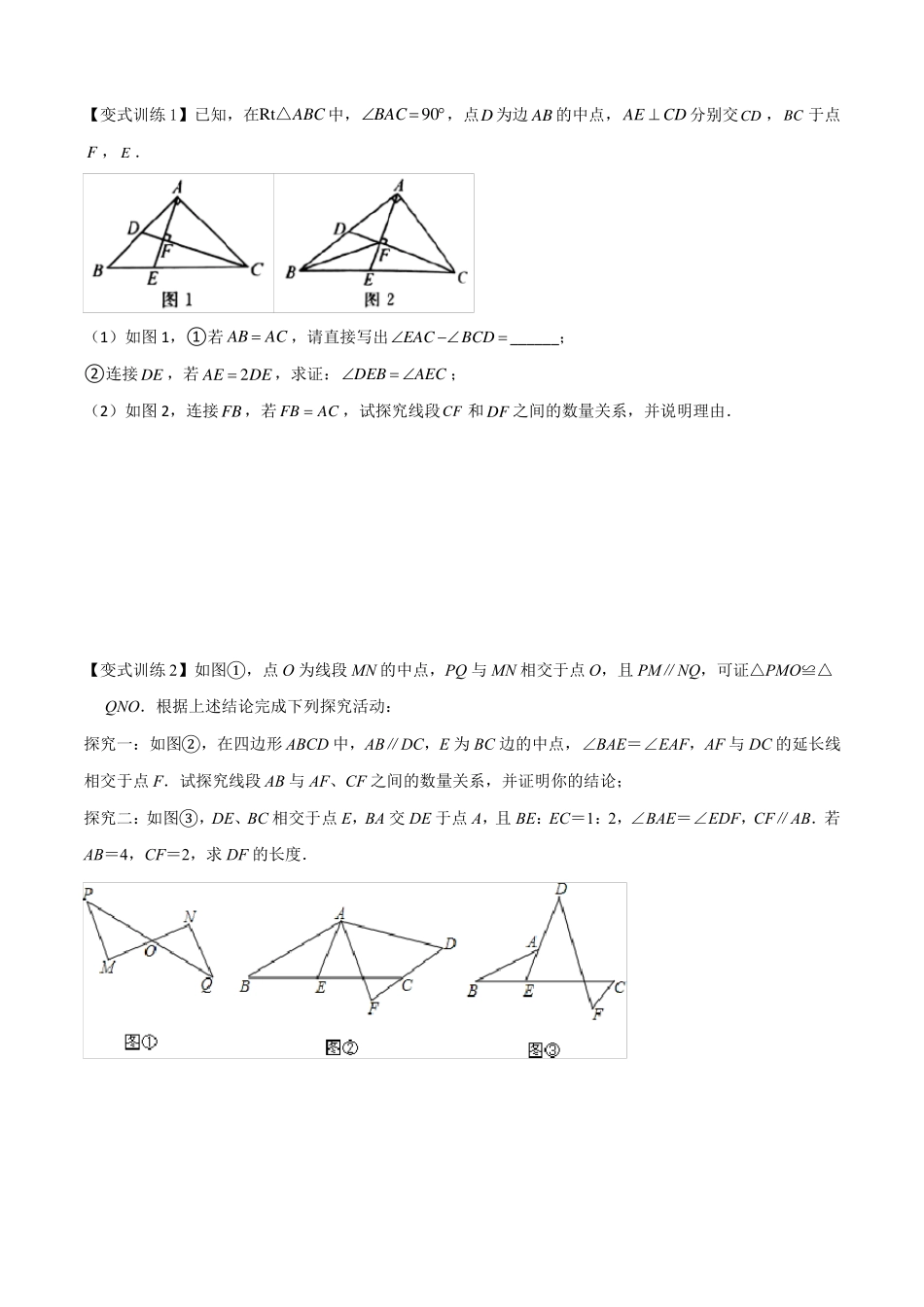
专题02单中点与双中点模型有关中点的知识点归纳：①三角形中线平分三角形面积；②直角三角形斜边上的中线等于斜边的一半；③等腰三角形“三线合一”的性质；④三角形中位线平行且等于第三边的一半.在题干中，出现一个中点时，我们通常想到中线；两个中点时，想到中位线。模型一、双中点-中位线模型如图，D、E、F分别为△ABC三边中点，连接DE、DF、EF，则，，.例.如图，在Rt△ABC中，△ACB＝90°，AC＝BC，过点C作CD△AB，垂足为D，点E为BC的中点，AE与CD交于点F，若DF的长为2，则AE的长为（）3A．2B．22C．5D．25【变式训练1】如图，在△ABC的两边AB、AC向形外作正方形ABDE和ACFG，取BE、BC、CG的中点M、Q、N．求证：MQ＝QN．【变式训练2】如图，在平面直角坐标系中，OAB的顶点B在x轴正半轴上，顶点A和边AB的中点C均在函数y2x0的图象上，则OAB的面积为（）xA．2B．3C．4D．6【变式训练3】如图，在△ABC中，∠ACB＝60°，AC＝1，D是AB的中点，E是BC上一点，若DE平分△ABC的周长，则DE的长为.模型二、单中点-倍长中线模型例.如图，CE、CB分别是ABC与ADC的中线，且ACBABC，ACAB．求证：CD2CE．【变式训练1】已知，在Rt△ABC中，BAC90，点D为边AB的中点，AECD分别交CD，BC于点F，E．（1）如图1，①若ABAC，请直接写出EACBCD______；②连接DE，若AE2DE，求证：DEBAEC；（2）如图2，连接FB，若FBAC，试探究线段CF和DF之间的数量关系，并说明理由．【变式训练2】如图①，点O为线段MN的中点，PQ与MN相交于点O，且PM∥NQ，可证△PMO≌△QNO．根据上述结论完成下列探究活动：探究一：如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE＝∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的数量关系，并证明你的结论；探究二：如图③，DE、BC相交于点E，BA交DE于点A，且BE：EC＝1：2，∠BAE＝∠EDF，CF∥AB．若AB＝4，CF＝2，求DF的长度．【变式训练3】如图，过边长为3的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为．模型二、单中点-“三线合一”模型如图，在△ABC中，AB＝AC，D为BC的中点，连接AD，则AD平分∠BAC，AD是边BC上的高，AD是BC边上的中线（AD是角平分线、中线、垂线）.例.如图，在矩形ABCD中，E为CB延长线一点且AC＝CE，F为AE的中点，求证：BF⊥FD.【变式训练1】如图所示，在△ABC中，AB＝AC＝5，BC＝6，M为BC的中点，MN⊥AC于点N，则MN等于（）A.B.C.D.【变式训练2】半径为1的半圆形纸片，按如图方式沿AB折叠，使折叠后半圆弧的中点M与圆心O重合，求图中阴影部分面积？课后训练1.如图所示，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB＝8，MN＝3，则AC的长是（）A．122.如图，B．14O的半径为5，AB为弦，点C为C．16D．18的中点，若∠ABC＝30°，则弦AB的长为（）A.B.5C.D.3.如图，正方形ABCD和正方形EFCG的边长分别为3和1，点F，G分别在边BC，CD上，P为AE的中点，连接PG，则PG的长为．4．如图，已知△ABC中，点D在AB上，点E在AC的延长线上，且BD=CE，连接DE交BC于点G，若DG=GE，说明：△ABC为等腰三角形．5．如图所示，已知在ABC中，D是AB的中点，DCAC，cosDCB4，求sinA．56.如图，在四边形ABCD中，E为AB上的一点，△ADE和△BCE都是等边三角形，AB、BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN的形状.7.如图，在△ABC中，BC＝22，BD⊥AC于点D，CE⊥AB于E，F、G分别是BC、DE的中点，若ED＝10，求FG的长.8．已知，在Rt△ABC中，BAC90，点D为边AB的中点，AECD分别交CD，BC于点F，E．（1）如图1，①若ABAC，请直接写出EACBCD______；②连接DE，若AE2DE，求证：DEBAEC；（2）如图2，连接FB，若FBAC，试探究线段CF和DF之间的数量关系，并说明理由．