非线性系统例题VIP免费

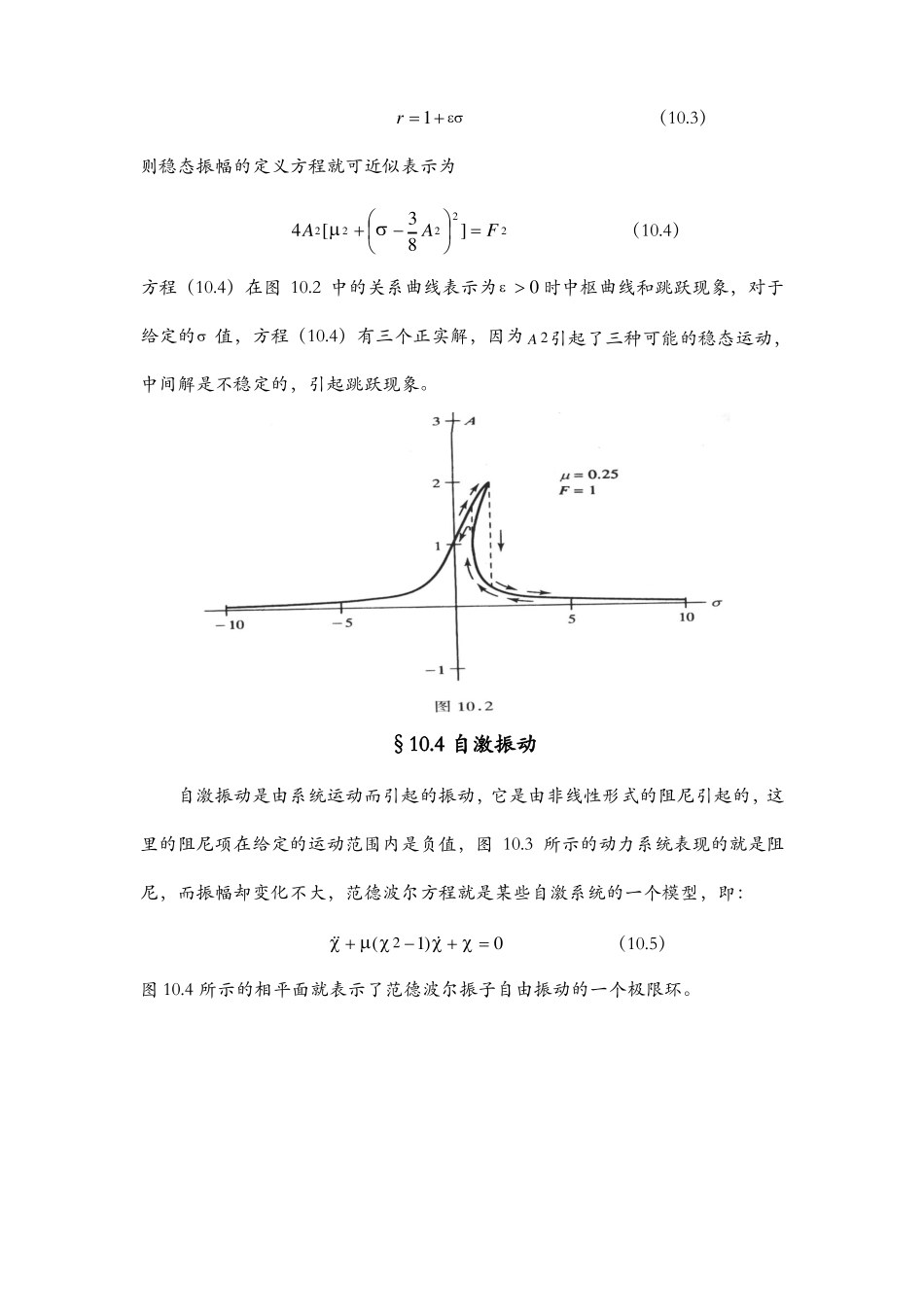
第十章非线性系统§10.1与线性系统的差异线性系统与非线性系统的不同之处在于：1.非线性系统的运动是由一个非线性微分方程控制的，但是很多非线性方程都不存在精确解。2.一个非线性系统可能不只一个平衡点，而平衡点可能是稳定的，也可能是不稳定的。3.非线性系统是否存在稳态运动取决于初始条件。4.非线性系统的自由振动周期由初始条件决定，这就意味着自由振动的频率依赖于自由振动的振幅。5.非线性系统的共振出现在激发频率不同于系统的线性固有频率处，在一个三维非线性系统中，当激发频率为系统线性固有频率的1/3时，产生超频共振；当激发频率为系统线性固有频率近三倍时，就产生亚频共振。6.线性叠加原理不能用来分析受多频激励的非线性系统，共振的组合是对应于激发频率的近似组合。7.对应于固有频率的近似组合，在多自由度的连续系统中存在内共振。8.在非线性系统中，周期激励可能会引起非周期响应，由于一些特定的参数值，这种混沌运动出现在很多非线性系统中。§10.1定性分析状态平面或相位平面是速度和位移在整个运动过程中的关系曲线，通过在平衡点的邻域内将控制微分方程线性化，可以检验平衡点的性质及其稳定性（见题10.2），平衡点的各种类型如图10.1所示。§10.3达芬方程达芬方程23Fsinrt（10.1）是一个无量纲方程。它作为一个模型可用于求解三维非线性系统。如果为正，则表示一个硬弹簧的响应；如果为负，则表示一个软弹簧系统的响应。一个系统自由振动的振幅关系由达芬方程决定，它可以用扰动方法近似表示为：31A2O(2)（10.2）8其中是固有频率的无量纲化（对于线性系统=1），A是振幅，分析共振附近达芬方程的受迫响应可以设r1（10.3）则稳态振幅的定义方程就可近似表示为34A[A2]F2（10.4）8222方程（10.4）在图10.2中的关系曲线表示为0时中枢曲线和跳跃现象，对于给定的值，方程（10.4）有三个正实解，因为A2引起了三种可能的稳态运动，中间解是不稳定的，引起跳跃现象。§10.4自激振动自激振动是由系统运动而引起的振动，它是由非线性形式的阻尼引起的，这里的阻尼项在给定的运动范围内是负值，图10.3所示的动力系统表现的就是阻尼，而振幅却变化不大，范德波尔方程就是某些自激系统的一个模型，即：(21)0（10.5）图10.4所示的相平面就表示了范德波尔振子自由振动的一个极限环。例题10.1单摆运动的非线性方程的无量纲化形式为sin0（i）推导定义运动相平面的广义方程；1条件下的轨线；（ii）求在0,（iii）单摆的最大摆角是多少？解:（i）令2，则ddddddtdtddtd从而微分方程就可以写成对求积分，则得dsin0d12cosC2其中C是一个积分常数。1（ii）要求当0时，1，则C，从而解出22cos1（iii）当0时，最大摆角6010.2令0代表非线性系统的平衡位置，取0来分析在平衡点邻域内系统的运动。通过在平衡点处线性化微分方程，来确定平衡点的类型及其稳定性。解：设控制微分方程的形式为：f(,)0若0代表一个平衡点，则f(0,0)0。将0代入微分方程，得：f(0,)0用泰勒级数展开，得：f(0,0)ff0(0,0)(0,0)加上平衡条件并略去高阶项线性化得：0方程的解可记为：ff(0,0)，(0,0)C1e1tC2e2t其中1和2是方程220的解，平衡点的类型及其稳定性讨论如下：（1）若1或2其一有正实部，则从平衡点出发的扰动无限大，故解不稳定。（2）若1和2都是正实数且同号，则平衡点为节点（稳定或不稳定。（3）若错是实数且同号，则平衡点为鞍点（不稳定）。（4）若1和2为共轭复数，则平衡点为焦点（稳定或不稳定）。（5）若1和2都是纯虚数，则平衡点是中点。10.3确定摆动方程所有平衡点的类型及其稳定性。解：单摆运动的非线性...