高中物理牛顿第二定律——板块模型解题基本思路VIP免费

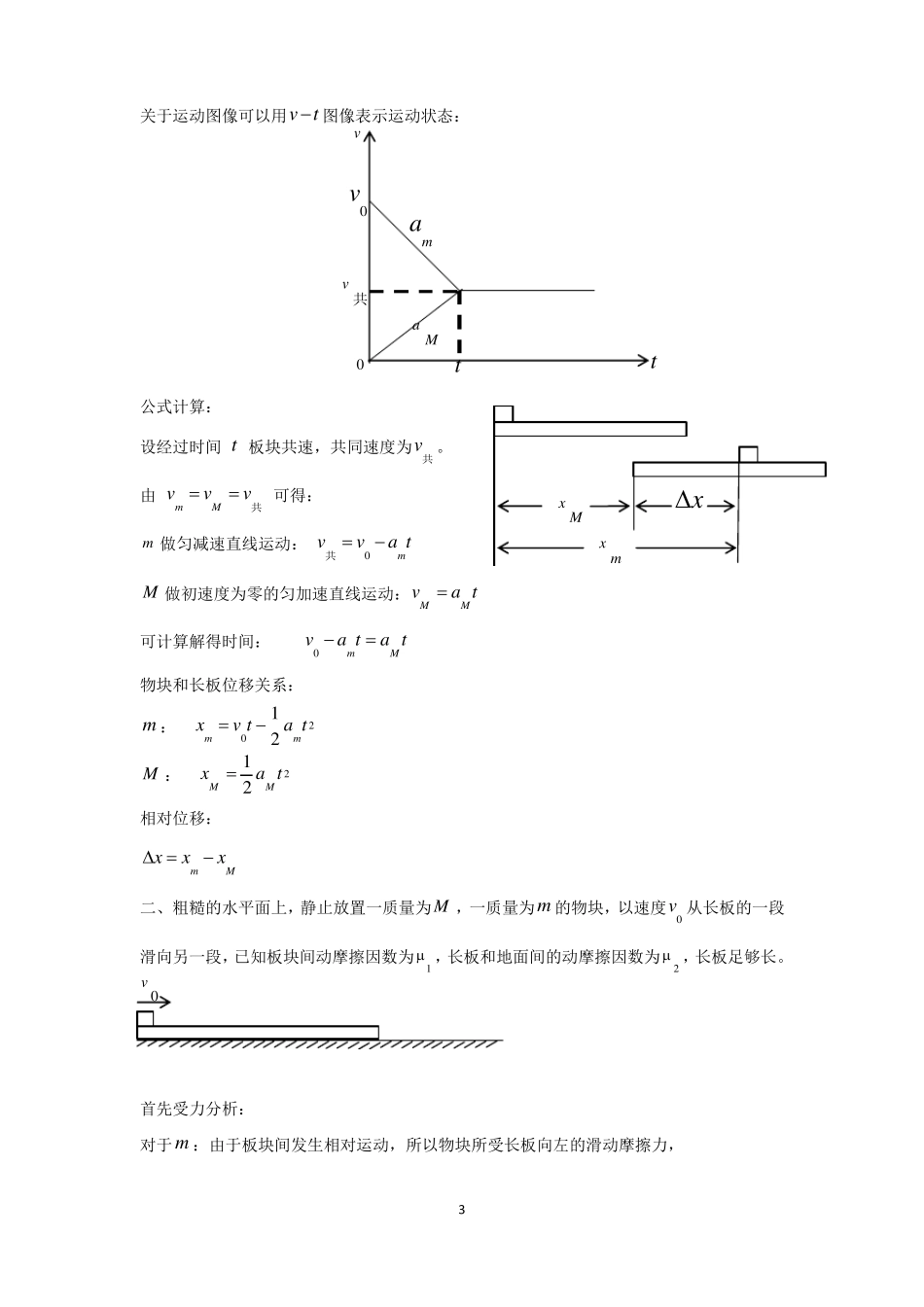
高中物理基本模型解题思路——板块模型（一）本模型难点：（1）长板下表面是否存在摩擦力，摩擦力的种类；静摩擦力还是滑动摩擦力，如滑动摩擦力，FN的计算（2）物块和长板间是否存在摩擦力，摩擦力的种类：静摩擦力还是滑动摩擦力。（3）长板上下表面摩擦力的大小。（二）在题干中寻找注意已知条件：（1）板的上下两表面是否粗糙或光滑（2）初始时刻板块间是否发生相对运动（3）板块是否收到外力F，如受外力F观察作用在哪个物体上（4）初始时刻物块放于长板的位置（5）长板的长度是否存在限定1一、光滑的水平面上，静止放置一质量为M，长度为L的长板，一质量为m的物块，以速度v0从长板的一段滑向另一段，已知板块间动摩擦因数为。v0首先受力分析：对于m：由于板块间发生相对运动，所以物块所受长板向左的滑动摩擦力，即：FNf动mgFNmgf动FNamg（方向水平向左）fmam动由于物块的初速度向右，加速度水平向左，所以物块将水平向右做匀减速运动。对于M：由于板块间发生相对运动，所以长板上表面所受物块向右的滑动摩擦力，但下表面由于光滑不受地面作用的摩擦力。即：FNFNf动MgMgFNFNmgafF（方向水平向右）动MNMfMaM动由于长板初速度为零，加速度水平向右，所以物块将水平向右做匀加速运动。假设当vmvM时，由于板块间无相对运动或相对运动趋势，所以板块间的滑动摩擦力会突然消失。则物块和长板将保持该速度一起匀速运动。2关于运动图像可以用vt图像表示运动状态：公式计算：设经过时间t板块共速，共同速度为v共。由vmvMv共可得：vv0amv共aM0ttxMxxmm做匀减速直线运动：v共v0amtM做初速度为零的匀加速直线运动：vMaMt可计算解得时间：v0amtaMt物块和长板位移关系：1m：xmv0tamt221M：xMaMt22相对位移：xxmxM二、粗糙的水平面上，静止放置一质量为M，一质量为m的物块，以速度v0从长板的一段滑向另一段，已知板块间动摩擦因数为1，长板和地面间的动摩擦因数为2，长板足够长。v0首先受力分析：对于m：由于板块间发生相对运动，所以物块所受长板向左的滑动摩擦力，3即：FN1mgmgFNmgf动FNam1g（方向水平向左）fmam动由于物块的初速度向右，加速度水平向左，所以物块将水平向右做匀减速运动。对于M：由于板块间发生相对运动，所以长板上表面所受物块向右的滑动摩擦力，下表面受到地面施加方向向左的摩擦力f的作用。即：FNf1mgFNMg由于长板所受的上表面向右的滑动摩擦力1mg和下表面地面所施加的最大静摩擦力大小关系未知，这里我们认为最大静摩擦力等于滑动摩擦力，所以我们要进行讨论：（1）当1mg2(Mm)g时：M仍然保持静止不动，m以加速度am做匀减速直线运动。（2）当1mg2(Mm)g时：M则产生一定的加速度：1mg2(Mm)gMaM，可求得M的加速度aM，方向向右。所以M将做初速度为零，加速度aM的匀加速直线运动，设经过时间t1二者速度相等，即vmvMv共解得时间：v0amt1aMt1解得二者共同的速度：v共1m位移：xmv0t1amt1224M位移：xM1aMt122二者在此过程中发生的相对位移：xxmxM当二者速度相同时，无相对运动，所以二者间滑动摩擦力突然消失，但由于长板下表面为粗糙，假设二者可以一起匀减速运动：mM：2(Mm)g(Mm)a共解得：a共2g由于2g1g，所以假设成立。当二者速度相同时，二者共同以加速度a共做匀减速运动，不再发生相对运动。共同匀减速时间：t2v共a共关于运动图像可以用vt图像表示运动状态：三、光滑的水平面上，静止放置一质量为M的长板，长板上静止放置一质量为m的物块，现对物块施加一外力F，板块间动摩擦因数为，假设长板与物块无相对运动一起加速，所以我们可以采用整体法来进行求解：vv0amv共aM0a共t1t1t2tFF(Mm)a当外力F增大时，整体的加速度a增大，说明长板和物块的加速度同时增大，但对于m：由于受到外力F的作用作为动力来源，所以m的加速度无最大值。但对于M：由于加速度的来源是m施加的静摩擦力产生，二者间的静摩擦力存在最大值，所以当二者间静摩擦力达到最大值时M的加速度也就存...