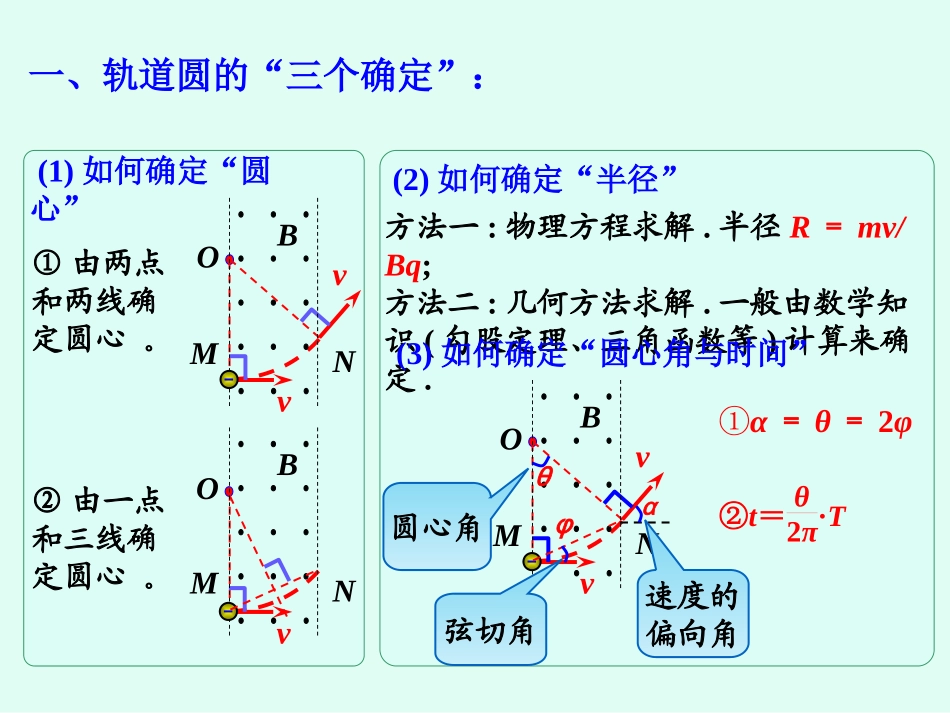
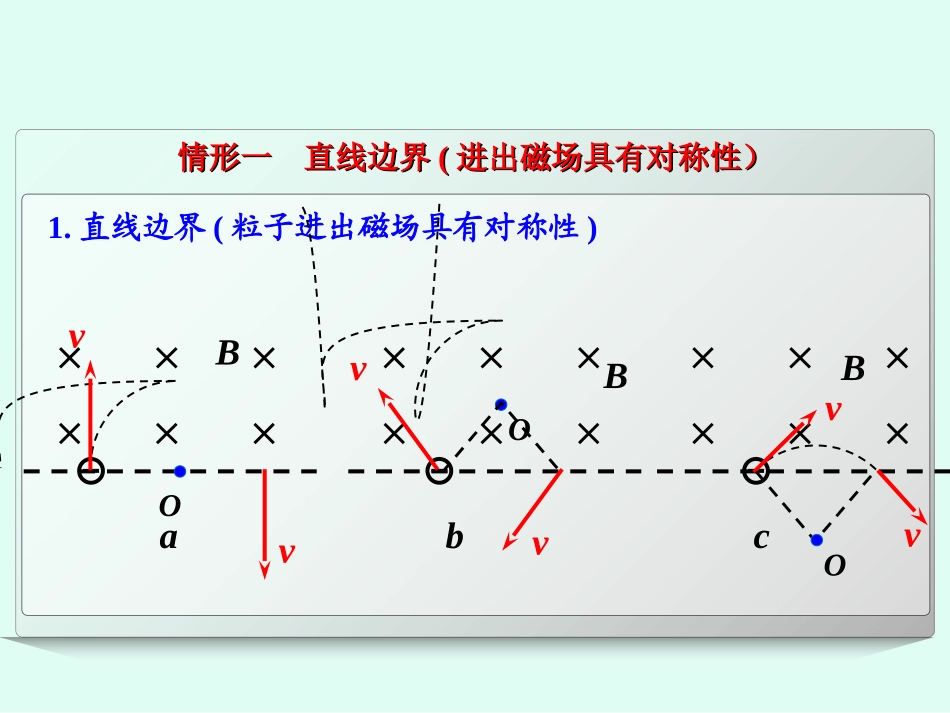
(1)如何确定“圆心”①由两点和两线确定圆心。vvBNMO②由一点和三线确定圆心。vBNMO(2)如何确定“半径”方法一:物理方程求解.半径R=mv/Bq;方法二:几何方法求解.一般由数学知识(勾股定理、三角函数等)计算来确定.(3)如何确定“圆心角与时间”vvBNMOθφα圆心角速度的偏向角弦切角①α=θ=2φ②t=θ2π·T一、轨道圆的“三个确定”:情形一直线边界情形一直线边界((进出磁场具有对称性)进出磁场具有对称性)1.直线边界(粒子进出磁场具有对称性)vOOBBvvvvBvOabc【例1】如图,直线MN上方存在范围足够大的磁感应强度为B的匀强磁场,一质子(质量为m、电荷量为e)以速度v从O点沿与MN成30°角的方向射入磁场中,若不计质子重力,则()A.质子从磁场中射出时距O点的距离为mvqBB.质子从磁场中射出时距O点的距离为3mvqBC.质子在磁场中运动的时间为3πm5qBD.质子在磁场中运动的时间为5πm3qBvr(1)半径:R=mv/Bq(2)运动时间:t=θ2π·T情形二情形二平行边界平行边界((存在临界条件存在临界条件))情形三情形三圆形边界圆形边界特点:沿径向射入必沿径向射出.【例2】如图示,半径为R的圆形区域内存在垂直纸面向外的匀强磁场,C、D是水平线与圆周的交点,且CD=R,AO是水平半径。甲、乙两粒子从A点以不同速度沿AO方向同时垂直射入匀强磁场中,甲、乙两粒子恰好同时分别击中C、D两点,不计粒子重力和粒子间的相互作用,则甲、乙两粒子的速度之比为()A.33B.32C.12D.23甲乙O1O212(1)粒子刚进入磁场时,所受洛伦兹力的方向怎样?在磁场中运动情况怎样?(2)“粒子射出磁场与射入磁场时运动方向间的夹角为60°”隐含了什么条件?(3)怎样画辅助线并由几何关系求半径?【例3】如图,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外,一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为R2.已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)().A.qBR2mB.qBRmC.3qBR2mD.2qBRm审题设疑v60°带电粒子在有界磁场中的常用几何关系规律方法(1)四个点:入射点、出射点、轨迹圆心和入射速度直线与出射速度直线的交点.(2)三个角:速度偏转角、圆心角、弦切角,其中偏转角等于圆心角,也等于弦切角的2倍.