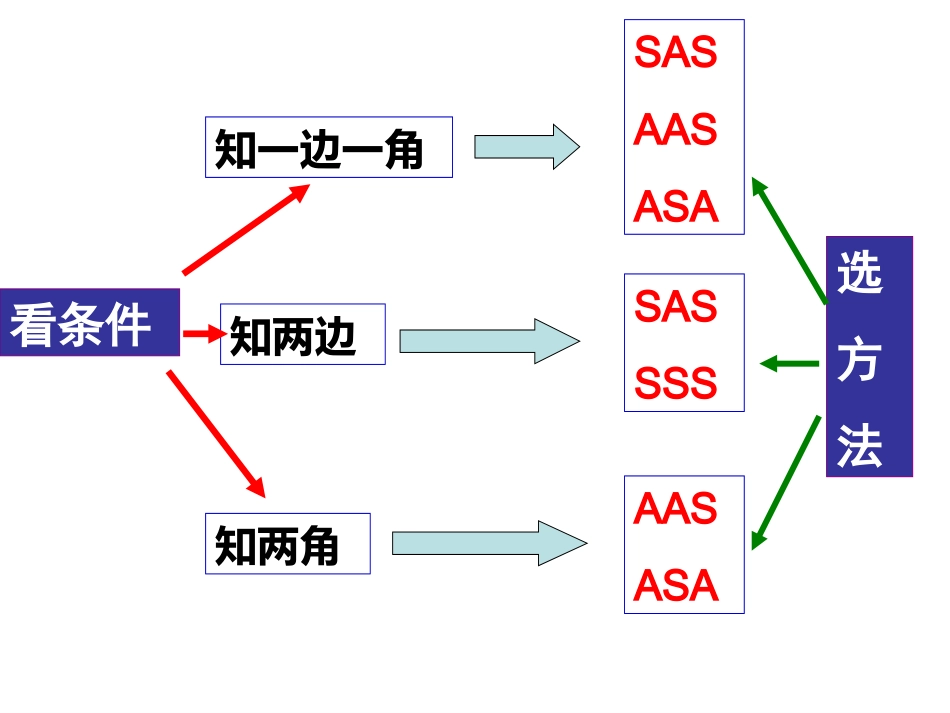
第26课时全等三角形茶陵腰陂中学:孟宪南2、三角形全等的判定及其方法1、全等三角形的定义SAS,ASA,AAS,SSS直角三角形(4+1)非直角三角形SAS,ASA,AAS,SSS,HL注意:“边边角”不可用!看条件知一边一角SASAASASA知两边SASSSS知两角AASASA选方法三角形全等1、对应边相等3、三角形全等的性质2、对应角相等3、周长、面积相等4、对应的高、中线角平分线相等,探究一探索三角形全等的条件或结论(开放性问题)P72例1如图,给出的四组条件①AB=DE,BC=EF,AC=DF②AB=DE,∠B=∠E,BC=EF③∠B=∠E,BC=EF,∠C=∠F④AB=DE,AC=DF,∠B=∠E能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组ABCDEFSSSSASASAC【变式】:P72课前2如图,已知AB=AC,要使△ABE≌△ACD,应添加的条件是_______________________(添加一个条件即可).∠B=∠C或AE=AD或∠AEB=∠ADC注意:1、题中已知一边和一角(隐含的条件公共角∠A)注意:答案不唯一,任选一个探究二全等三角形的性质与判定的综合应用CP72例2、如图△ABO与△CDO关于点O中心对称,点E、F在线段AC上,且AF=CE.求证:DF=BEABEFDo思路:先定三角形,再证三角形全等注意:1、图形对称转化点对称或全等2、隐含条件对顶角证明一CABEFDoOBODBOEDOFOEOF∵△ABO与△CDO关于点O中心对称∴OA=OC,OB=OD又∵AF=CE,∴OF=OE,在△BOE与△DOF中,∴△BOE≌△DOF(SAS),∴BE=DF.【变式1】:P73优化2如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DCABCDE1证明二设法证明△ABE≌△CDF,可得BE=DF(略)CABEFDo【变式2】:P74优化3如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF(1)求证:BF=2AE(2)若CD=2,求AD的长.=AC与P72课前练习1对比,你发现了什么?【1】(2013株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;(2)若∠EOD=30°,求CE的长.【2】(2014•株洲)如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).(1)求证:△ACE≌△AFE;(2)求tan∠CAE的值.(1)法一、用AAS证明△ACE≌△AFE(1)法二、用HL证明△ACE≌△AFE【3】(2015•怀化)已知如图,在△ABC中,DE、DF是三角形△ABC的中位线,连接EF、AD,其交点为O,求证(1)△CDE≌△DBF;(2)OA=OD.ABCDFEO【4】(2013泸州)如图在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①图中全等三角形只有两对;②CD+CE=2AO③△ABC的面积等于四边形CDOE的面积;④222ADBEOPOC;其中正确的结论有()A、1个B、2个C、3个D、4个AOBDCEPC教材母题——湘教版八上P88T9已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:(1)AE∥FB;(2)DE=CF.(1)因为AD=BC,所以AC=BD.又因为AE=BF,CE=DF,所以△AEC≌△BFD,所以∠A=∠B,所以AE∥BF.(2)由(1)知△AEC≌△BFD,所以∠FDC=∠ECD.因为CD=CD,CE=DF,所以△CDE≌△DCF,所以DE=CF.证明60°如图,已知△ABC三个内角的平分线交于点O,点D在C的延长线上,且DC=BC,AD=AO.若∠BAC=80°,求∠BCA的度数C解析∵△ABC三个内角的平分线交于点O,∴∠ACO=∠BCO.在△COD和△COB中,CD=CB,∠OCD=∠OCBCO=CO,,∴△COD≌△COB,∴∠D=∠CBO.∵∠BAC=80°,∴∠BAD=100°,∠BAO=40°,∴∠DAO=140°.∵AD=AO,∴∠D=20°,∴∠CBO=20°,∴∠ABC=40°,∴∠BCA=60°.