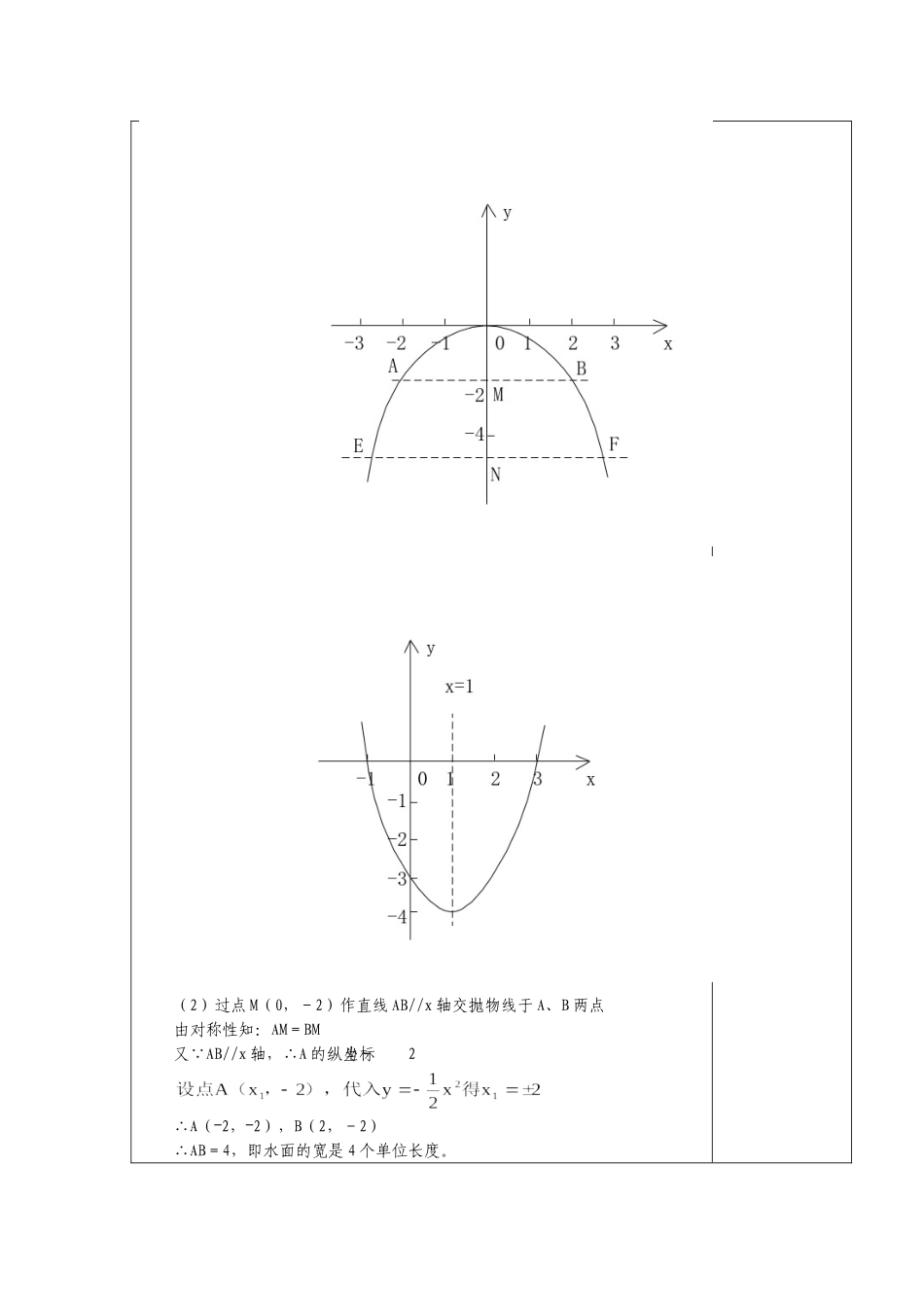
课题二次函数的应用课型新授教学目标知识与技能能通过解一元二次方程求抛物线与x轴的交点坐标,会利用待定系数法求二次函数的解析式,会利用二次函数的图象求一元二次方程的近似解。会运用二次函数解决实际问题.过程与方法经历运用二次函数解决实际问题的过程:问题情境——建模——解释体会二次函数是解决实际问题的重要模型情感与态度感受数学的应用价值,敢于面对在解决最优化问题时碰到的困难,并有独立克服困难和运用知识解决问题的成功体验。教学重点利用二次函数的性质,解决实际问题教学难点图象法解一元二次方程,利用二次函数的图象、性质,解决实际生活中相关的问题教具准备教学过程教师活动学生活动【主要内容】(一)二次函数解析式的确定:二次函数解析式有三种形式:例如:根据下列条件求二次函数的解析式:(1)二次函数的图象经过点A(-1,-6),B(1,-2),C(2,3)(2)已知抛物线顶点为(-1,-3)且与y轴交点(0,-5)(3)已知抛物线与x轴交于点A(-1,0),B(1,0)且经过点M(0,1)解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0)将(-1,-6),(1,-2),(2,3)分别代入得:(2) 抛物线顶点为(-1,-3)(3) 点A(-1,0),B(1,0)是抛物线与x轴的交点∴设抛物线的解析式为y=a(x+1)(x-1)将M(0,1)代入上式得:+1=a(0+1)(0-1)∴a=-1∴抛物线的解析式为y=-(x+1)(x-1)即y=-x2+1(二)二次函数y=ax2+bx+c与一元二次方程的联系二次函数与一元二次方程的联系就是“形”与“数”的有机结合。当二次函数的表达式y=ax2+bx+c(a≠0)中,y=0时,恰好是一元二次方程ax2+bx+c=0(a≠0)而y=0时,方程的根是二次函数与x轴交点的横坐标,此外,利用一元二次方程,可以研究二次函数的图象与x轴交点的情况,方程有实数解的个数,就是函数图象与x轴交点的个数。即方程ax2+bx+c=0的根的判别式(Δ=b2-4ac)可以判断抛物线y=ax2+bx+c与x轴交点的个数。当Δ>0时,抛物线与x轴有两个交点。当Δ=0时,抛物线与x轴有唯一一个交点(即顶点在x轴上)当Δ<0时,抛物线与x轴没有交点。(三)从实际问题中建立数学模型实际生活中的二次函数常见类型有以下几种:(1)利用实际问题构建二次函数关系式,如卫星运行轨道、桥洞等问题。(2)经济问题中最大值、最小值问题。(1)画出这条抛物线的图象。(2)利用图象求:当水平线离开抛物线顶点2个单位时,水面的宽是多少个单位长度?(3)利用图象求:当水面宽是6个单位长度时,水平线离开抛物线顶点的距离是多少个单位长度。解:(1)如图(2)过点M(0,-2)作直线AB//x轴交抛物线于A、B两点由对称性知:AM=BM又 AB//x轴,∴A的纵坐标为-2∴A(―2,―2),B(2,-2)∴AB=4,即水面的宽是4个单位长度。(3)作EF//x轴,交抛物线于E、F两点,交y轴于N点 EF=6,∴FN=3即F点到y轴的距离为3即水面离抛物线顶点的距离是4.5个单位长度。【典型例题】解:例2.已知y=x22x3――,问x为何值时,y>0?x为何值时,y<0?分析:利用函数图象求不等式的解集,找出抛物线与x轴的交点,再根据交点坐标及图象的位置,写出不等式的解集。解:先确定抛物线y=x22x3――的对称轴,顶点坐标及与x轴交点坐标。∴对称轴为x=1,顶点坐标(1,-4)∴抛物线与x轴交点为(-1,0),(3,0)画出抛物线的草图(如图)当y>0时,即纵坐标为正,x轴上方图象上的点。左边,x轴上方的点:x<1―右边,x轴上方的点:x>3∴当x<-1或x>3时,y>0当y<0时,即纵坐标为负,也就是x轴下方图象上的点∴当-1