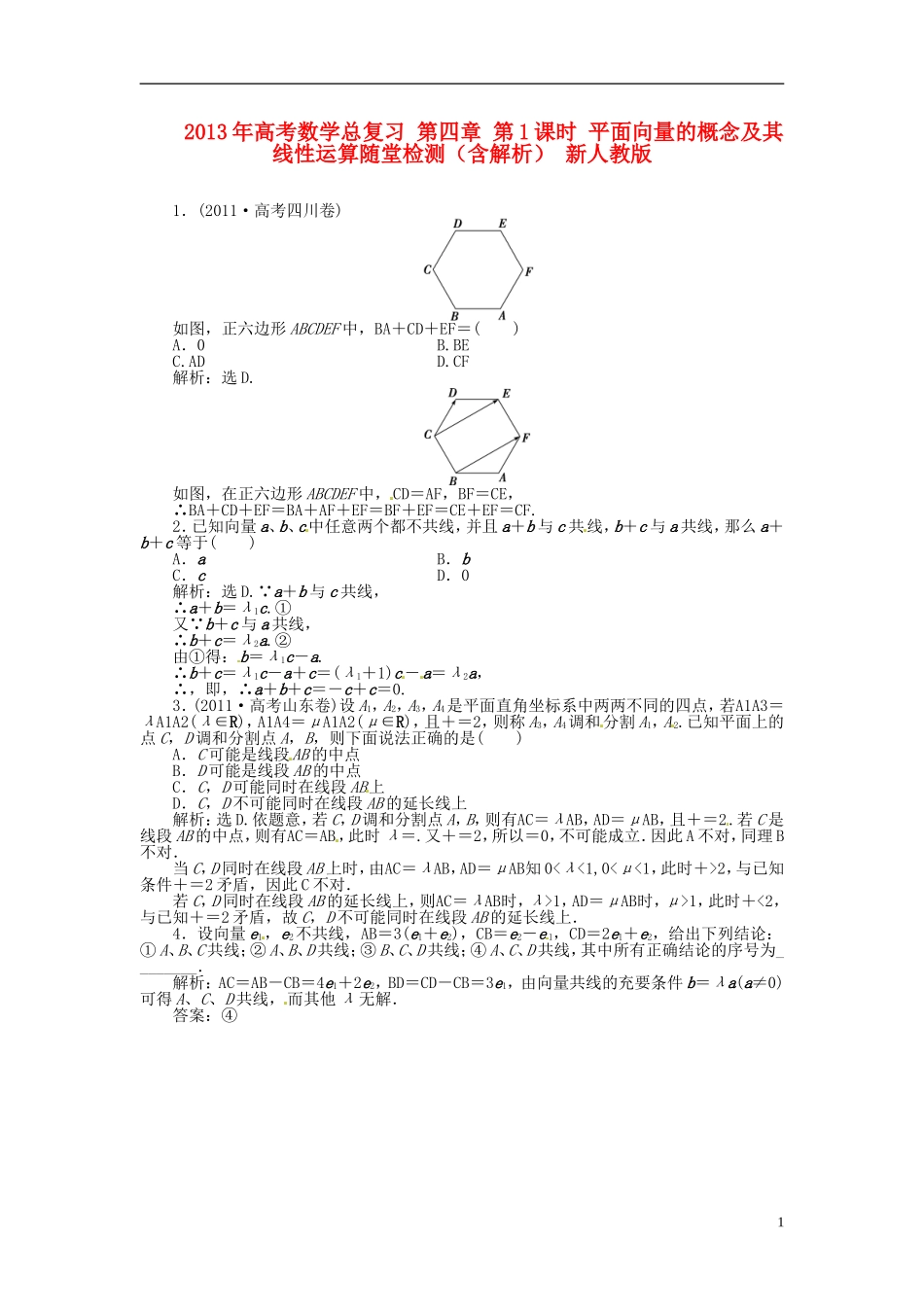
2013年高考数学总复习第四章第1课时平面向量的概念及其线性运算随堂检测(含解析)新人教版1.(2011·高考四川卷)如图,正六边形ABCDEF中,BA+CD+EF=()A.0B.BEC.ADD.CF解析:选D.如图,在正六边形ABCDEF中,CD=AF,BF=CE,∴BA+CD+EF=BA+AF+EF=BF+EF=CE+EF=CF.2.已知向量a、b、c中任意两个都不共线,并且a+b与c共线,b+c与a共线,那么a+b+c等于()A.aB.bC.cD.0解析:选D.∵a+b与c共线,∴a+b=λ1c.①又∵b+c与a共线,∴b+c=λ2a.②由①得:b=λ1c-a.∴b+c=λ1c-a+c=(λ1+1)c-a=λ2a,∴,即,∴a+b+c=-c+c=0.3.(2011·高考山东卷)设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若A1A3=λA1A2(λ∈R),A1A4=μA1A2(μ∈R),且+=2,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则下面说法正确的是()A.C可能是线段AB的中点B.D可能是线段AB的中点C.C,D可能同时在线段AB上D.C,D不可能同时在线段AB的延长线上解析:选D.依题意,若C,D调和分割点A,B,则有AC=λAB,AD=μAB,且+=2.若C是线段AB的中点,则有AC=AB,此时λ=.又+=2,所以=0,不可能成立.因此A不对,同理B不对.当C,D同时在线段AB上时,由AC=λAB,AD=μAB知0<λ<1,0<μ<1,此时+>2,与已知条件+=2矛盾,因此C不对.若C,D同时在线段AB的延长线上,则AC=λAB时,λ>1,AD=μAB时,μ>1,此时+<2,与已知+=2矛盾,故C,D不可能同时在线段AB的延长线上.4.设向量e1,e2不共线,AB=3(e1+e2),CB=e2-e1,CD=2e1+e2,给出下列结论:①A、B、C共线;②A、B、D共线;③B、C、D共线;④A、C、D共线,其中所有正确结论的序号为________.解析:AC=AB-CB=4e1+2e2,BD=CD-CB=3e1,由向量共线的充要条件b=λa(a≠0)可得A、C、D共线,而其他λ无解.答案:④1