2015高中数学2.1.2指数函数及其性质课件2新人教A版必修1VIP免费

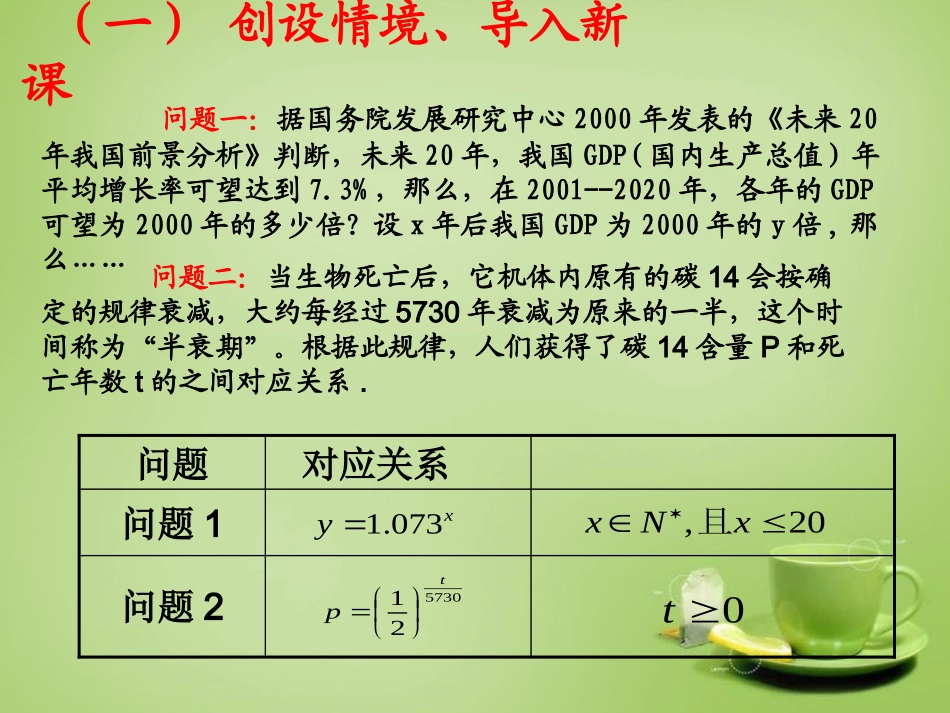
2.1.2指数函数及其性质问题一：据国务院发展研究中心2000年发表的《未来20年我国前景分析》判断，未来20年，我国GDP(国内生产总值）年平均增长率可望达到7.3%，那么，在2001--2020年，各年的GDP可望为2000年的多少倍？设x年后我国GDP为2000年的y倍,那么……问题二：当生物死亡后，它机体内原有的碳14会按确定的规律衰减，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”。根据此规律，人们获得了碳14含量P和死亡年数t的之间对应关系.问题2问题1对应关系问题xy073.120,xNx且573021tp0t（一）创设情境、导入新课1：上述两种对应关系能否构成函数关系？•（1）幂的形式都一样；•（2）幂的底数都是一个正常数；•（3）幂的指数都是一个变量。2：上述两个函数有什么样的共同特征？能构成函数关系想一想？问题2问题1定义域对应关系问题xy073.120,xNx且573021tp0t（二）师生互动、探究新知底为常数指数为自变量一般地、函数叫做指数函数,其中x为自变量，定义域为R。xay,a(0)a1且1.指数函数的概念：探究：探究：定义中为什么要规定定义中为什么要规定01aa且探讨:若不满足上述条件会怎么样呢?xay（1）若a=0,则当x＞0时，.0xa当x≤0时,无意义.xa（2）若a＜0,则对于x的某些数值，可使无意义。如，这时对于……，在实数范围内函数值不存在.(2)x1124,xxxa以上三种情况都不利于我们研究指数函数，所以规定：a>0且a≠1.（3）若a=1,则对于任何,是一个常量，没有研究的必要性.xR1xa练习1：求下列函数的定义域；23xy（1）.211xy（2）2x解:（1）由有意义，得x-2≥0即x≥2，∴原函数定义域为{x|x≥2}.（2）由x1有意义，得x≠0，∴原函数定义域为{x|x∈R且x≠0}.练习2：某种细胞分裂时，由1个分裂成2个，2个分成4个、、、依此类推,写出1个这样的细胞分裂x次后，得到的细胞个数y与x的函数解析式.一个细胞分裂次数第一次第二次第三次第四次第x次…...细胞总数y21222324…...2xy=2x解析式x问题一：你能类比前面讨论函数性质时的思路，提出研究指数函数性质的方法吗？能力培养，探求新知问题二：怎样得到指数函数的图象？函数图像数形结合列表描点连线由特殊到一般的规律动动手：请同学们画一画下面两个函数的图像。12xy1(2)2xy84211812143210-1-2-3x2xy-3-2-10123x87654321yy=2x(3,8)(2,4)(1,2)(0,1)21(-1,)41(-2,)81(-3,)-3-2-10123x87654321yy=()x213210-1-2-3x12xy1248121418-3-2-10123x87654321yy=2xy=()x21(3,8)(2,4)(1,2)(0,1)21(-1,)41(-2,)81(-3,)思考1:函数的图像与的图像有什么关系？可否利用的图像画出的图像？xy2xy21xy2xy21(-3,8)(-2,4)(-1,2)(0,1)41(2,)21(1,)81(3,)函数y=2x的图像与的图像关于y轴对称.y=()x21xy0y=()xy=()x2131y=2xy=3x思考2:如图四个指数函数图像，当底数大于0小于1和大于1时，图像在画法上有什么特点？思考3：通过图像，你能发现指数函数的哪些共同特征？当底数大于0小于1时，图像自左向右是下降的；当底数大于1时，图像自左向右是上升的。1.图像向左、向右是无限延伸的。2.图像都在x轴的上方。3.都过定点（0，1）。(0,1)2.指数函数的图像及性质xay01图像定义域值域性定点质单调性yx0y=1(0,1)yx0y=1(0,1)(0,+∞)RR(0,+∞)(0,1)即x=0时,y=1。在R上是单调增函数在R上是单调减函数例6、已知指数函数的图像经过点（3，π）求(0),(1),(-3)的值。）且10()(aaaxfxfff（一）典例分析xaxf)(),,3(,)3(f解：因为的图像过点所以即,3a解得,31a于是.)(3xxf所以，.1)3(,)1(,1)0(13310fff三、典例分析、巩固训练例7：比较下列各题中两个值的大小：35.27.17.11和）（2.01.08.08.02和）（1.33.09.07.13和）（目的是应用指数函数的单调性“比较两个数的大小”，熟悉指数函数的性质，使学生形成利用函数观点解决问题的意识。三、典例分析、巩固训练（一）典例分析比较下列各题中两个值的大小：①5271..，371.解：利用函数单调性,5271..与37...